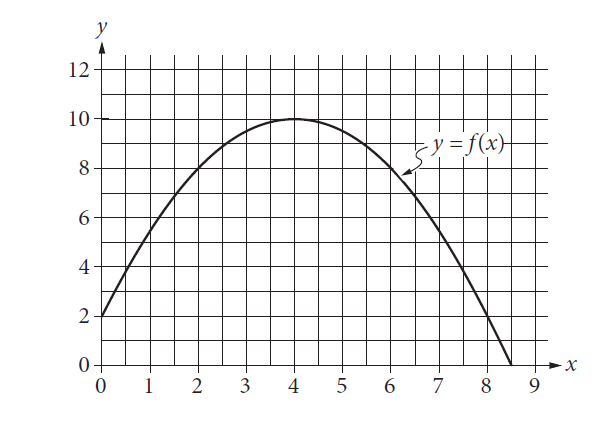
The graph of the function f, defined by f(x)=−12(x−4)2+10, is shown in the xy-plane above. If the function g (not shown) is defined by g(x) = −x + 10, what is one possible value of a such that f (a) = g(a) ?
The correct Answer is:2 AND 8
Substituting x = a in the definitions for f and g gives f(a)=−12(a−4)2+10 and g(a)=-a+10, respectively. If f(a)=g(a) , then −12(a−4)2+10=−a+10 Subtracting 10 from both sides of this equation gives −12(a−4)2=−a . Multiplying both sides by -2 gives (a−4)2=2a. Expanding (a−4)2 gives a2−8a+16=2a. Combining the like terms on one side of the equation gives a2−10a+16=0. One way to solve this equation is to factor a2−10a+16 by identifying two numbers with a sum of −10 and a product of 16. These numbers are −2 and −8, so the quadratic equation can be factored as (a − 2)(a − 8) = 0. Therefore, the possible values of a are either 2 or 8. Either 2 or 8 will be scored as a correct answer.
Alternate approach: Graphically, the condition f (a) = g(a) implies the graphs of the functions y = f (x) and y = g(x) intersect at x = a. The graph y = f (x) is given, and the graph of y = g(x) may be sketched as a line with y-intercept 10 and a slope of −1 (taking care to note the different scales on each axis). These two graphs intersect at x = 2 and x = 8.
Similar Questions
The figure above shows the graph of function h. If function f is defined by f(x)=h(2x)+1, what is the value of f(−1)?
View Solution
The figure above shows the complete graph of the function f in the xy-plane. The function g (not shown) is defined by g(x) = f (x) + 6.What is the maximum value of the function g ?
View Solution
Knowledge Check
If function g is defined by g(x)=x-1 and 2g(c)=10, what is the value of g(3c)?
A6B9C15D17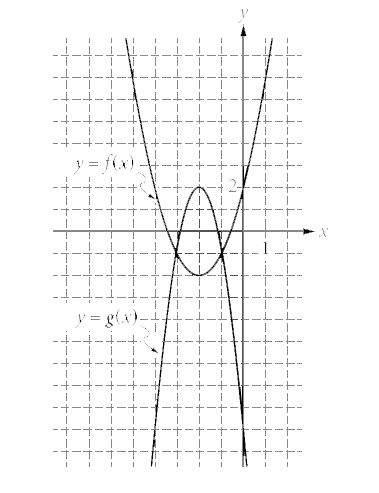
Graphs of the functions f and g are shown in the xy-plane above. For which of the following values of x does f(x)+g(x)=0 ?A−3B−2C−1D0The function f and g are defined as f(x)=2x−3 and g(x) = x + 3//2.Forwˆvalueofyisf(y) = g(y- 3) ?
A1B3/2C2D3
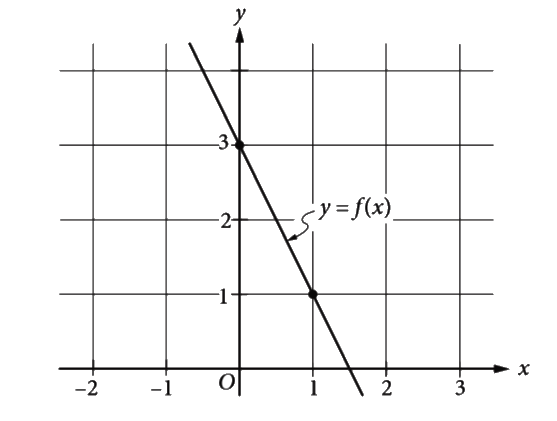
The graph of the linear function f is shown in the xy-plane above. The graph of the linear function g (not shown) is perpendicular to the graph of f and passes through the point (1,3). What is the value of g(0) ?
View Solutionf:R→R is a function defined by f(x)=10x−7,ifg=f−1 then g(x)=
View SolutionA function f is defined by f(x) =x2+1. Find f(0), f(5), f(10).
View Solution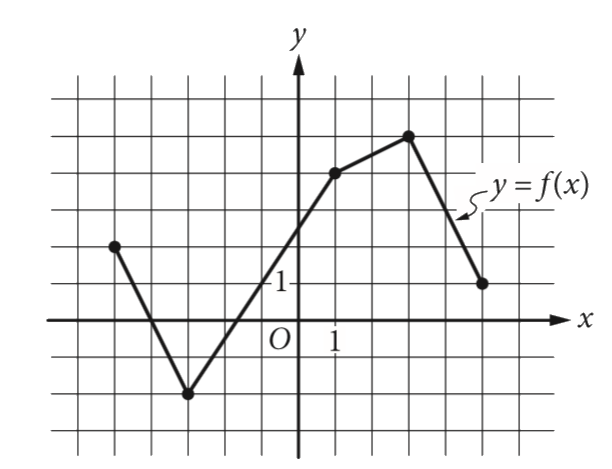
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?
View SolutionThe function f and g are defined as f(x,y)=2x+yandg(x,y)=x+2y. What is the value of f(3,4) ?
View Solution
