An electron is liberated from a hot filament and attracted by an anode at 1200 V. What is its speed when it strike the anode?(e=1.6×10−19C)
The correct Answer is:2.1×107ms−1
To find the speed of the electron when it strikes the anode at 1200 V, we can use the principle of conservation of energy. The gain in kinetic energy of the electron will be equal to the loss in potential energy as it moves from the filament to the anode.
1. Identify the initial and final energies:
- The electron is initially at rest when it is liberated from the hot filament, so its initial kinetic energy (KE_initial) is 0.
- The potential energy (PE_initial) at the filament is negative because it is in an electric field, but we can consider it as a reference point.
2. Calculate the potential energy at the anode:
- The potential energy at the anode (PE_final) can be calculated using the formula:
PE=V⋅q
where V=1200V (the voltage of the anode) and q=−1.6×10−19C (the charge of the electron).
- Thus, the potential energy at the anode is:
PEfinal=1200V⋅(−1.6×10−19C)=−1.92×10−16J
3. Calculate the change in potential energy:
- The change in potential energy (ΔPE) from the filament to the anode is:
ΔPE=PEfinal−PEinitial
- Since we can consider the potential energy at the filament to be 0 (as a reference), we have:
ΔPE=−1.92×10−16J−0=−1.92×10−16J
4. Relate the change in potential energy to kinetic energy:
- The gain in kinetic energy (KE) is equal to the loss in potential energy:
KE=−ΔPE=1.92×10−16J
5. Use the kinetic energy formula to find speed:
- The kinetic energy of the electron can also be expressed as:
KE=12mv2
where m=9.11×10−31kg (mass of the electron) and v is the speed we want to find.
- Setting the two expressions for kinetic energy equal gives:
1.92×10−16=12(9.11×10−31)v2
6. Solve for v2:
- Rearranging the equation gives:
v2=2⋅1.92×10−169.11×10−31
7. Calculate v:
- Performing the calculation:
v2=3.84×10−169.11×10−31≈4.22×1014
- Taking the square root:
v≈√4.22×1014≈2.06×107m/s
Final Answer:
The speed of the electron when it strikes the anode is approximately 2.06×107m/s.
- The electron is initially at rest when it is liberated from the hot filament, so its initial kinetic energy (KE_initial) is 0.
- The potential energy (PE_initial) at the filament is negative because it is in an electric field, but we can consider it as a reference point.
- The potential energy at the anode (PE_final) can be calculated using the formula:
PE=V⋅q
where V=1200V (the voltage of the anode) and q=−1.6×10−19C (the charge of the electron).
- Thus, the potential energy at the anode is:
PEfinal=1200V⋅(−1.6×10−19C)=−1.92×10−16J
- The change in potential energy (ΔPE) from the filament to the anode is:
ΔPE=PEfinal−PEinitial
- Since we can consider the potential energy at the filament to be 0 (as a reference), we have:
ΔPE=−1.92×10−16J−0=−1.92×10−16J
- The gain in kinetic energy (KE) is equal to the loss in potential energy:
KE=−ΔPE=1.92×10−16J
- The kinetic energy of the electron can also be expressed as:
KE=12mv2
where m=9.11×10−31kg (mass of the electron) and v is the speed we want to find.
- Setting the two expressions for kinetic energy equal gives:
1.92×10−16=12(9.11×10−31)v2
- Rearranging the equation gives:
v2=2⋅1.92×10−169.11×10−31
- Performing the calculation:
v2=3.84×10−169.11×10−31≈4.22×1014
- Taking the square root:
v≈√4.22×1014≈2.06×107m/s
The speed of the electron when it strikes the anode is approximately 2.06×107m/s.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENIALBOOK - NN GHOSHCHAPTER - ELECTRIC FIELD AND POTENIALEXERCISE - EXERCISE-B
35 Videos
- ELECTRIC FIELD AND POTENIALBOOK - NN GHOSHCHAPTER - ELECTRIC FIELD AND POTENIALEXERCISE - EXERCISE-B
35 Videos
- DYNAMO, MOTOR, TRANSFORMERBOOK - NN GHOSHCHAPTER - DYNAMO, MOTOR, TRANSFORMEREXERCISE - EXERCISE
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NN GHOSHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERICISES-B
18 Videos
Similar Questions
Knowledge Check
Two insulting plates are both uniformly charged in such a way that the potential difference between them is V2−V1=20V. (i.e., plate 2 is at a higher potential). The plates are separated by d=0.1m and can be treated as infinity large. An electron is released from rest on the inner surface of plate 1. What is its speed when it hits plate 2? (e=1.6×10−19C, me=9.11×10−31kg)
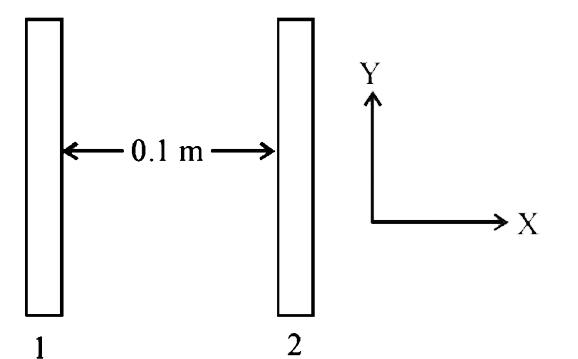 A(a) 2.65×106m/sB(b) 7.02×1012m/sC(c) 1.87×106m/sD(d) 32×10−19m/s
A(a) 2.65×106m/sB(b) 7.02×1012m/sC(c) 1.87×106m/sD(d) 32×10−19m/sAn electron is accelerated under a potential difference of 64 V, the de-Brogile wavelength associated with electron is [e=−1.6×10−19C,me=9.1×10−31kg,h=6.623×10−34Js]
A1.53ÅB2.53ÅC3.35ÅD4.54ÅA cathode emits 1.8×1017 electron per second and all the electrons reach the anode when it Is given a positive potential of 400V. Given e=1.6×10−19C, the maximum anode current is .
A2.88mAB28.8mAC7.2mAD6.4mA
An electron beam energes from an accelerator with kinetic energy 100eV. What is its de-Broglie wavelength?
[m=9.1×10−31kg,h=6.6×10−34Js,1eV=1.6×10−19J]
View SolutionSuppose that the particle in Q.33 is an electron projected with velocity vx=2.0×106ms−1. If E between the plates separated by 0.5cmis9.1×102N/C, where will the electron strike the upper plate ? (|e|=1.6×10−19C,me=9.1×10−31kg).
View SolutionSuppose that the particle in Question 1.33 is an electron projected with velocity vx=2.0×106ms−1 .If E between the plates separated by 0.5 cm is 9.1×102N/C , where will the electron strike the upper plate ? (|e|=1.6×10−19C,me=9.1×10−31kg)
View SolutionAn electron is accelerated under a potential difference of 182 V. the maximum velocity of electron will be (Given, charge of an electron is 1.6×10−19C ms−1 and its mass is 9.1×10−31kg)
View SolutionAn electron revolves in a circule at the rate of 1019 rounds per second. The rquivlent current is (e=1.6×10−19C)
View Solution
