Find the tension in the string holding a solid block of volume and density dipped in liquid and tied to the bottom of a container filled with liquid of density shown in figure
(i) When container is moving upwards with an acceleration .
(ii) When container is stationary .

Step by step video & image solution for Find the tension in the string holding a solid block of volume 1000 cm^(3) and density 0.8 gm//cm^(3) dipped in liquid and tied to the bottom of a container filled with liquid of density 1.2 gm//cm^(3) shown in figure (i) When container is moving upwards with an acceleration 4.9 m//s^(2). (ii) When container is stationary . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - practice Exercise 7.1
10 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Practice Exercise 7.2
8 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
Similar Questions
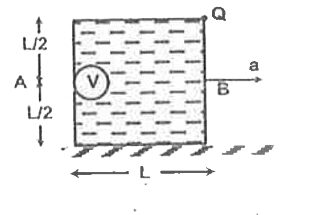
A small ball of volume V and density ρ is held inside a cubical container of side L filled with an ideal liquid of density 4ρ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given g=10m/s2
View SolutionA vessel contains two immiscible liquids of densit ρ1=1000kg/m3 and ρ2=1500kg/m3. A solid block of volume V=103m3 and density d=800kg/m3 is tied to one end of a string and the outer end is tied to the bottom of the vessel as shown in figure.
The block is immersed with two fifths of its volume in the liquid of lower density. The entire system is kept in an elavator which is moving upwards with an acceleration of a=g2. Find the tension in the string. brgt
View Solution
Knowledge Check
A wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
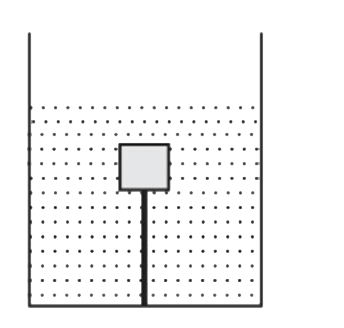 A2NB3NC5ND6N
A2NB3NC5ND6NA body having volume V and density ρ is attached to the bottom of a container as shown. Density of the liquid is d(>ρ). Container has a constant upward acceleration a. Tension in the string is
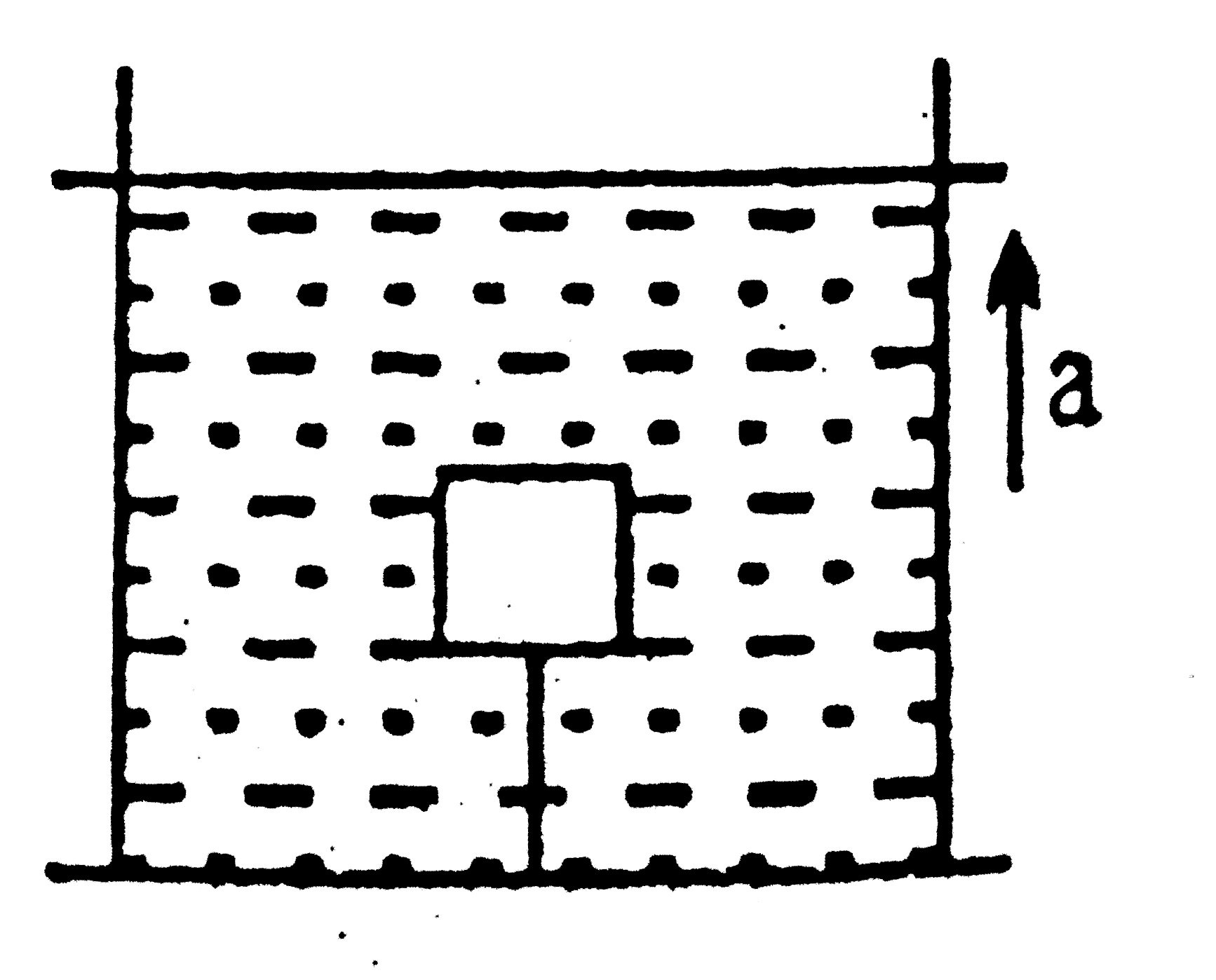 AV[Dg−ρ(g+a)]BV(g+a)(d−ρ)CV(d−ρ)gDnone
AV[Dg−ρ(g+a)]BV(g+a)(d−ρ)CV(d−ρ)gDnone
A mass m of volume V=10cm2 is tied with a string to the base of a container filled with a liquid of density (Pl=103kg/m3) as shown in the figure. The container is then accelerated with acceleration (ax=9m/s2) and (ay=2m/s2) a shown in the figure. [g=10(ms2) acceleration due to gravity] the net buoyancy force acting on the mass isA10 NB12 NC15 ND9 N
10g of a liquid of density 5gcm−3 is mixed with 12g of another miscible liquid of density 4gcm−3. Find the density of mixture.
View SolutionA body of mass 2 kg and volume 0.001m3 is in a fluid of density 4/3gm/cm3 . The fluid is at rest . Determine whether the body will float or sink in the fluid ? If it sinks , then find out the acceleration .
View SolutionA body of density 2.5g/cm3 is let free in a liquid of density 1.25g/cm3 . The downward acceleration of the of the body while sinking in the liquid is . _______
View SolutionThe tension in a string holding a solid block below the surface of a liquid (of density greater than that of solid) as shown in figure is T0 when the system is at rest. What will be the tension in the string if the system has an upward acceleration a?
 .
.
View SolutionA small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)

View Solution
