A thin uniform rod of length 2l and specific gravity 3/4 is hinged at one end to height l/2 above the surface of water, with the other end immersed. Find the inclination of rod in equilibrium
To solve the problem of finding the inclination of a thin uniform rod of length 2L and specific gravity 3/4, which is hinged at one end at a height of L/2 above the surface of water, with the other end immersed, we can follow these steps:
1. Identify the Parameters:
- Length of the rod, Lrod=2L
- Specific gravity of the rod, SG=34
- Height of the hinge above the water surface, h=L2
2. Determine the Density of the Rod:
- The density of water, ρwater.
- The density of the rod, ρrod=SG×ρwater=34ρwater.
3. Calculate the Weight of the Rod:
- The volume of the rod, V=A×2L (where A is the cross-sectional area).
- The mass of the rod, m=ρrod×V=34ρwater×A×2L.
- The weight of the rod, W=m×g=34ρwater×A×2L×g=32ρwaterAgL.
4. Determine the Length of the Submerged Part:
- Let x be the length of the part of the rod that is above water.
- The length of the submerged part is 2L−x.
5. Calculate the Buoyant Force:
- The volume of the submerged part, Vsub=A×(2L−x).
- The buoyant force, FB=ρwater×Vsub×g=ρwater×A×(2L−x)×g.
6. Set Up the Moment Equation:
- The center of mass of the rod is at L from the hinge.
- The center of buoyancy is at (2L−x)/2 from the hinge.
- Moment about the hinge (O):
FB⋅(L+(2L−x)2)−W⋅L=0
7. Substitute Values into the Moment Equation:
- Substitute FB and W:
ρwater⋅A⋅(2L−x)⋅g⋅(L+(2L−x)2)−32ρwaterAgL2=0
8. Cancel Common Terms:
- Cancel ρwater, A, and g:
(2L−x)⋅(L+(2L−x)2)−32L2=0
9. Solve for x:
- Rearranging gives:
(2L−x)(L+L−x2)=32L2
- Simplifying leads to:
4L2−2Lx−Lx+x22=32L2
- This simplifies to:
x22−3Lx+52L2=0
10. Use the Quadratic Formula:
- Solve for x using the quadratic formula:
x=−b±√b2−4ac2a
where a=12,b=−3L,c=52L2.
11. Find the Angle of Inclination:
- Use the triangle formed by the rod:
sinθ=L/2L⇒θ=sin−1(12)=30∘
Final Answer:
The inclination of the rod in equilibrium is θ=30∘.
---
- Length of the rod, Lrod=2L
- Specific gravity of the rod, SG=34
- Height of the hinge above the water surface, h=L2
- The density of water, ρwater.
- The density of the rod, ρrod=SG×ρwater=34ρwater.
- The volume of the rod, V=A×2L (where A is the cross-sectional area).
- The mass of the rod, m=ρrod×V=34ρwater×A×2L.
- The weight of the rod, W=m×g=34ρwater×A×2L×g=32ρwaterAgL.
- Let x be the length of the part of the rod that is above water.
- The length of the submerged part is 2L−x.
- The volume of the submerged part, Vsub=A×(2L−x).
- The buoyant force, FB=ρwater×Vsub×g=ρwater×A×(2L−x)×g.
- The center of mass of the rod is at L from the hinge.
- The center of buoyancy is at (2L−x)/2 from the hinge.
- Moment about the hinge (O):
FB⋅(L+(2L−x)2)−W⋅L=0
- Substitute FB and W:
ρwater⋅A⋅(2L−x)⋅g⋅(L+(2L−x)2)−32ρwaterAgL2=0
- Cancel ρwater, A, and g:
(2L−x)⋅(L+(2L−x)2)−32L2=0
- Rearranging gives:
(2L−x)(L+L−x2)=32L2
- Simplifying leads to:
4L2−2Lx−Lx+x22=32L2
- This simplifies to:
x22−3Lx+52L2=0
- Solve for x using the quadratic formula:
x=−b±√b2−4ac2a
where a=12,b=−3L,c=52L2.
- Use the triangle formed by the rod:
sinθ=L/2L⇒θ=sin−1(12)=30∘
The inclination of the rod in equilibrium is θ=30∘.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - practice Exercise 7.1
10 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Practice Exercise 7.2
8 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
Similar Questions
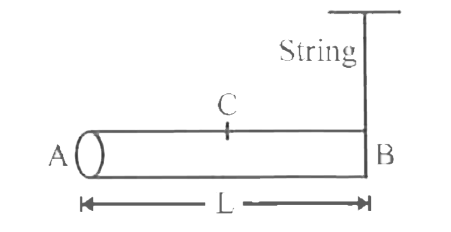
A uniform rod AB of length L and and weight Mg is hinged at one end A. The rod is kept in the horizontal position by a massless string. If the string is cut, then the angular acceleration of the rod will be
[M.I. of the rod about A is ML23]
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View Solution
Knowledge Check
A uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
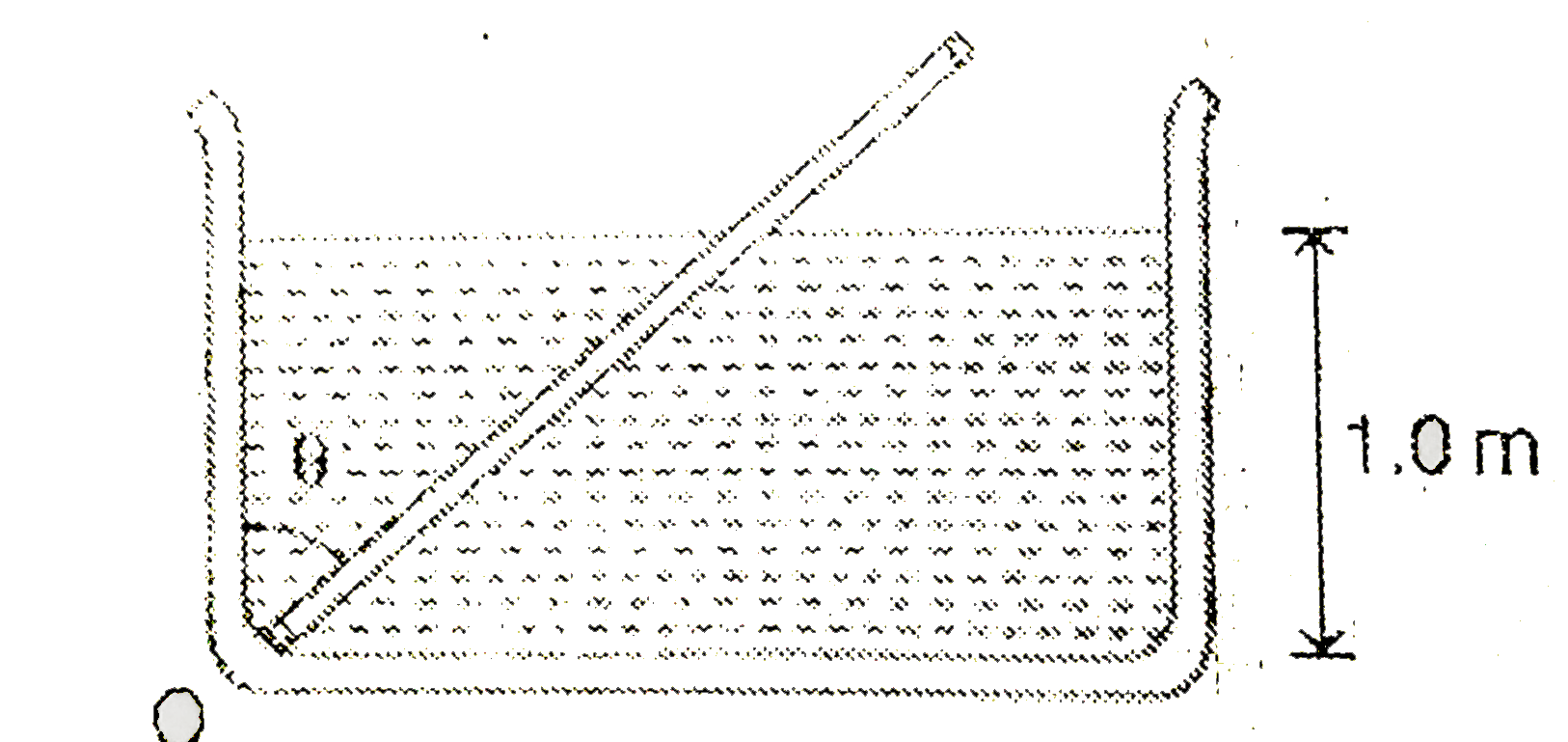 A10.2 N upwardsB4.2 N downwardsC8.3 N downwardsD6.2 N upwards
A10.2 N upwardsB4.2 N downwardsC8.3 N downwardsD6.2 N upwardsThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
A(l2−a2)/a2B(l2−a2)/2a2C(l2−a2)/3a2Dnone of these
A thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
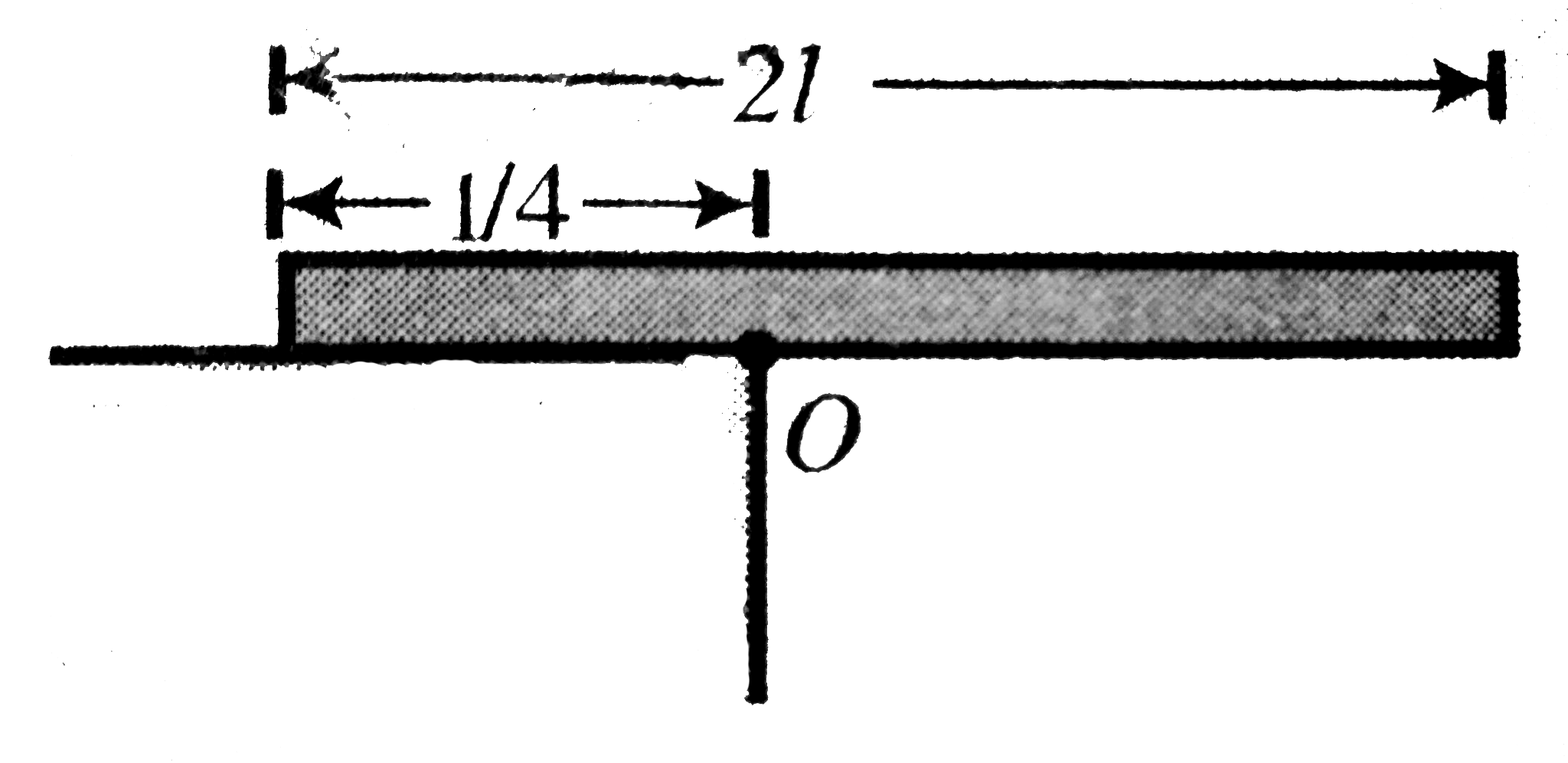
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
View SolutionA thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.
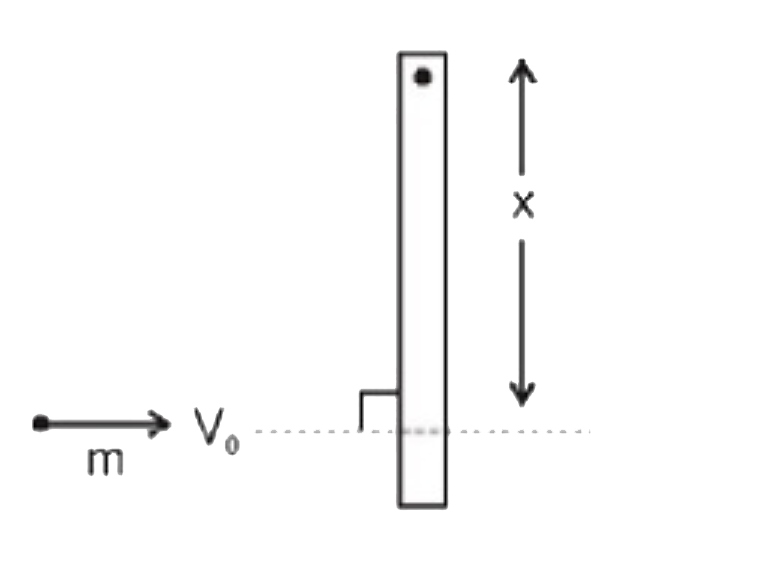
View SolutionA uniform rod of mass m and length L is hinged at one end and free to rotate in the horizontal plane. All the surface are smooth. A particle of same mass m collides with the rod with a speed V0. The coefficient of restitution for the collision is e=12. If hinge reaction during the collision is zero then the value of x is :
View Solution
