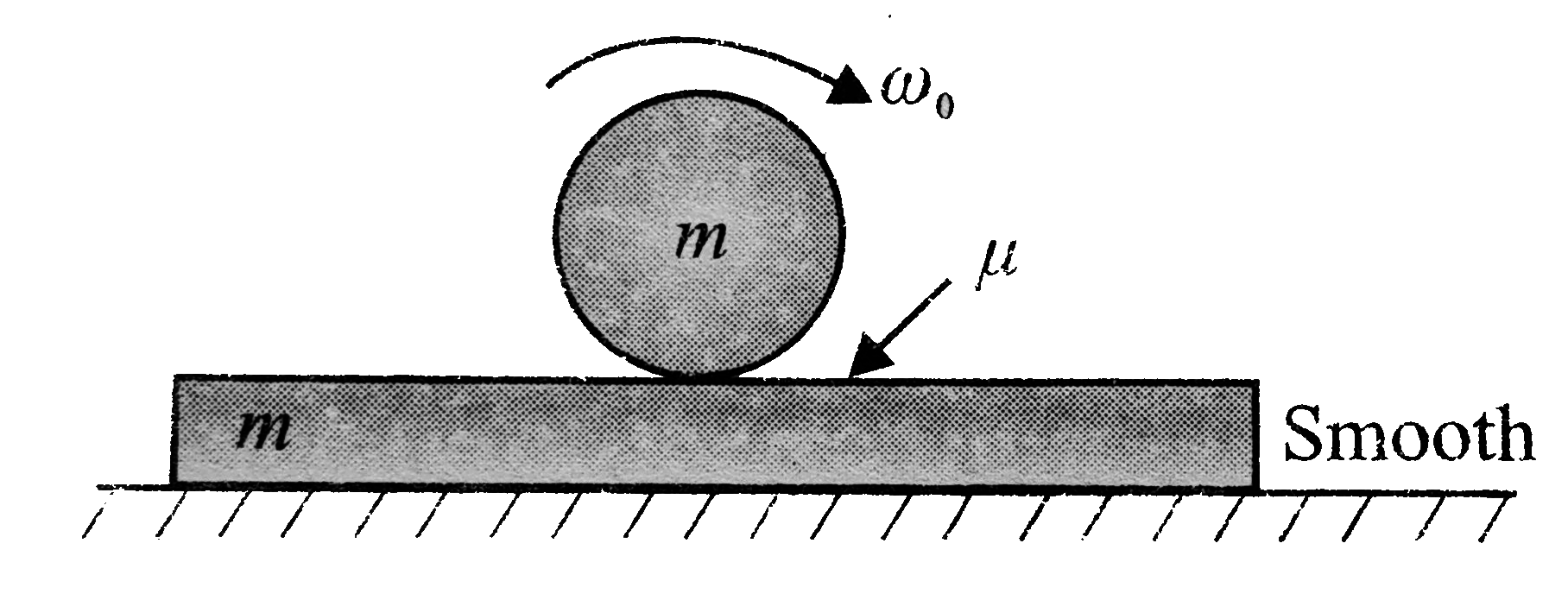
A sphere of mass m is given some angular velocity about a horizontal axis through the center, and gently placed on a plank of mass m. The coefficient of friction between the two is μ. The plank rests on a smooth horizontal surface. The intial acceleration of the sphere relative to the plank will be:
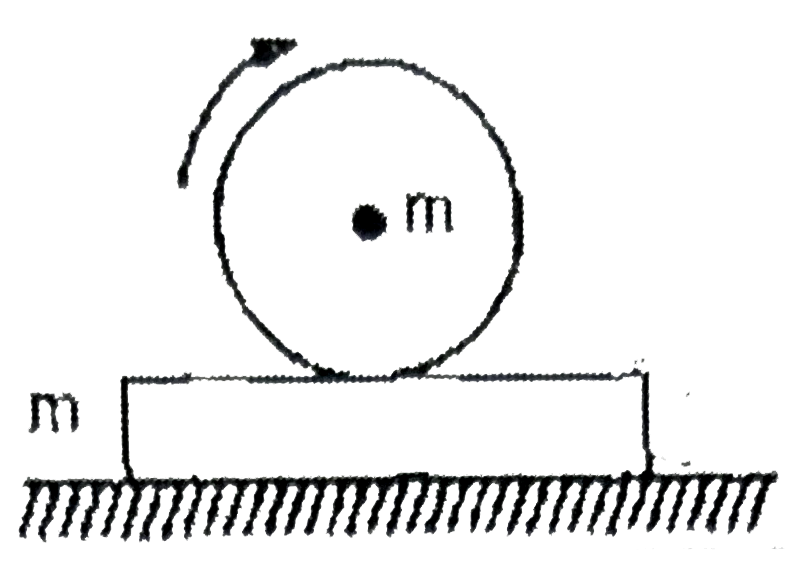
zero
μg
7/5μg
2μg
The correct Answer is:D
Step by step video, text & image solution for A sphere of mass m is given some angular velocity about a horizontal axis through the center, and gently placed on a plank of mass m. The coefficient of friction between the two is mu. The plank rests on a smooth horizontal surface. The intial acceleration of the sphere relative to the plank will be: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
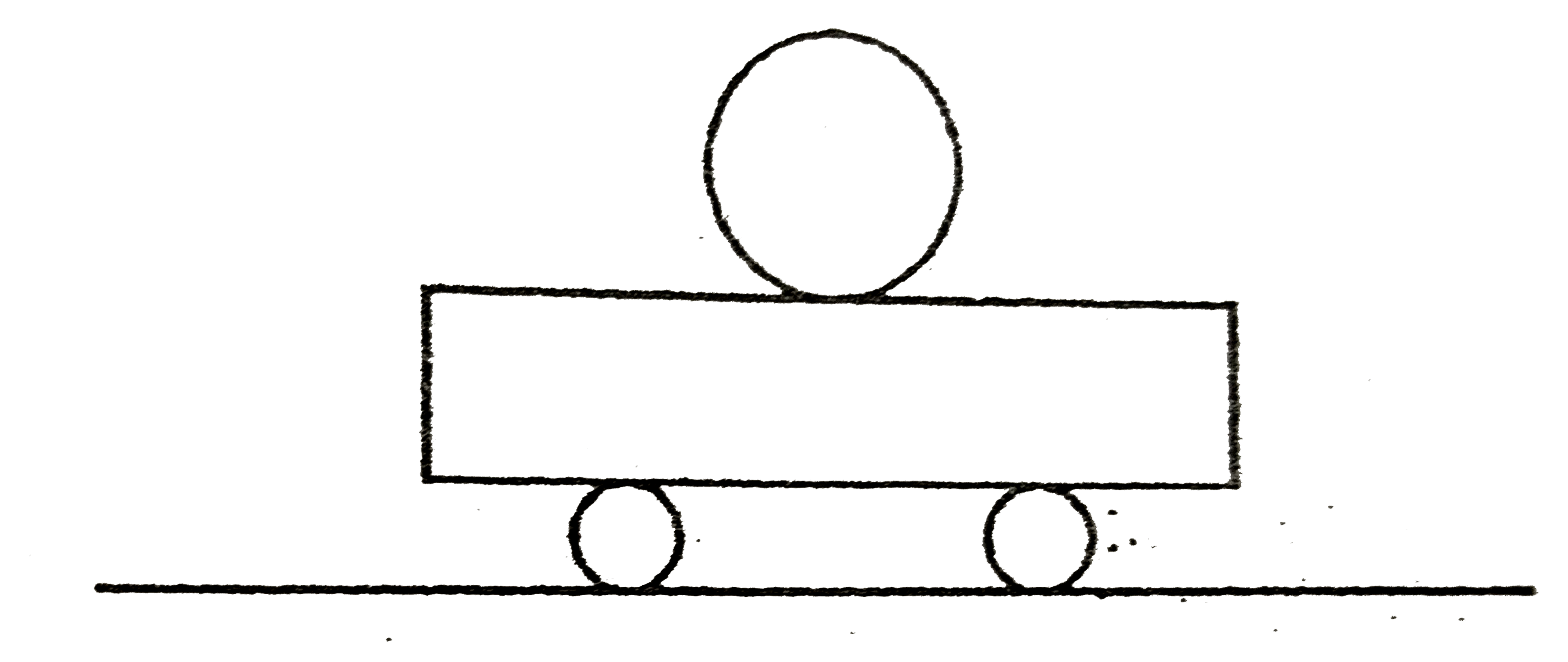
Angular acceleration of sphere is
View Solution
Knowledge Check
A sphere of mass m is given some angular velocity about a horizontal axis through its centre and gently placed on a plank of mass 'm'. The co-efficent of friction between the two is μ. The plank rests on a smooth horizontal surface. The initial acceleration of the centre of sphere relative to the plank will be
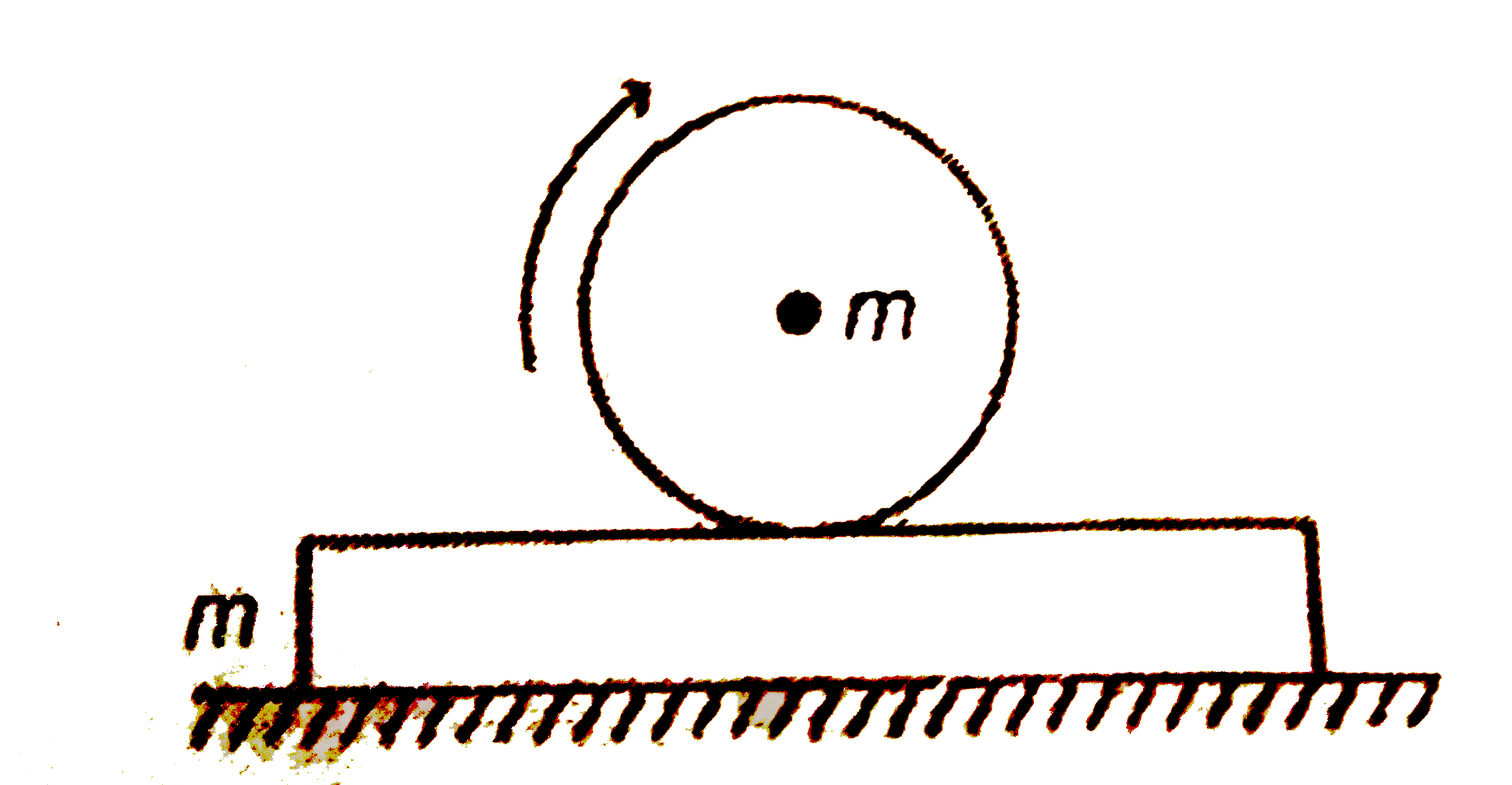 AzeroBμgC(7/5)μgD2μg
AzeroBμgC(7/5)μgD2μgA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.Aω20r281μgB2ω20r227μgC4ω20r281μgD2ω20r281μgA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
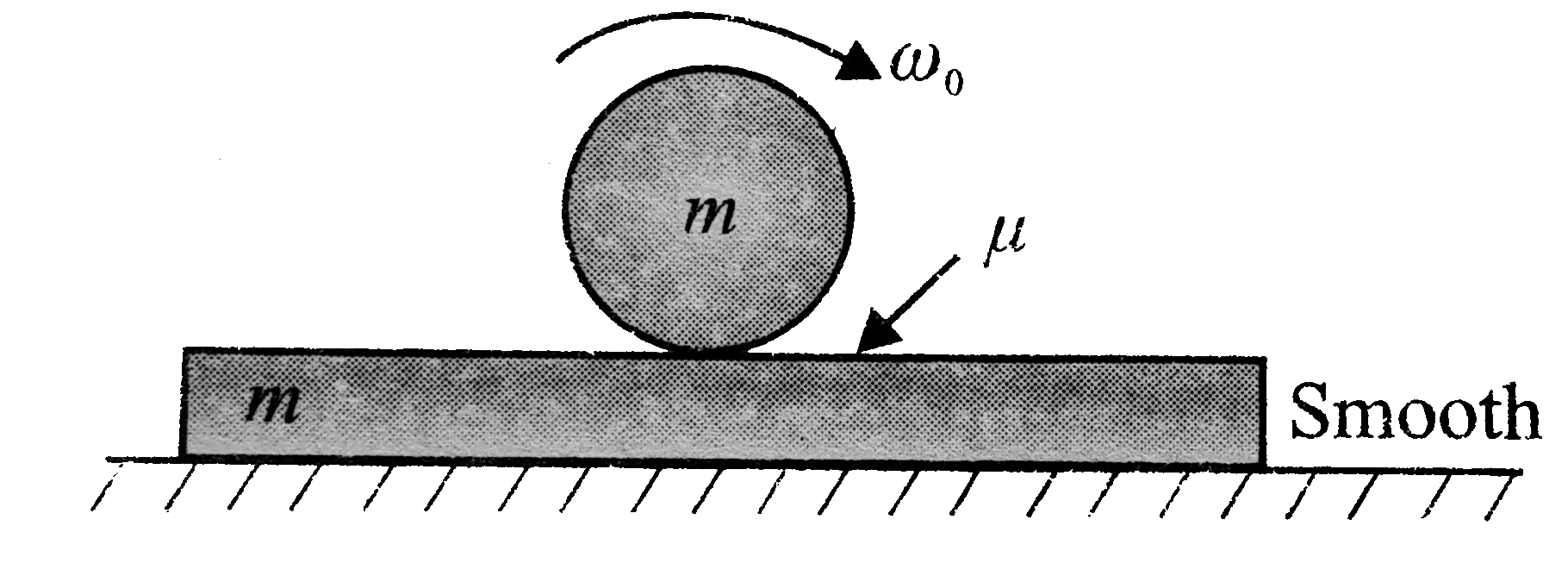
Find the velocity of the sphere after the pure rolling startsA2ω0r9Bω0r9Cω03D2ω0r3
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
Acceleration of centre of mass of sphere is
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling starts
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
Find the time t at which the pure roiling starts
View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :

View Solution
