The shorter the impact time of an impulse, the greater the force must be for the same momentum change and hence the greater the deformation of the object on which the foce acts. Wxplain on this basis the value of air bags which are intended to inflate during an automobile collision and reduce the possibility of fracture or death.
Step by step video & image solution for The shorter the impact time of an impulse, the greater the force must be for the same momentum change and hence the greater the deformation of the object on which the foce acts. Wxplain on this basis the value of air bags which are intended to inflate during an automobile collision and reduce the possibility of fracture or death. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Conceptual MCQ s single option correct
30 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Numerical MCQ s
75 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Practive Exercise
28 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
When the force on a object depends on the position of the object, we cannot find the work done by it on the object by simple multiplying the force by the displacement. The reason is that there is no one value for the force-it changes. So, we must find the work in tiny little displacements and then add up all the workk results. We effectively say, "Yes, the force varies over any given tiny little displacement. but the variation is so small we can approximate the force as being constant during the displacements infinitesimal, then our error becomes infinitesimal and the result becomes precise. But, to add an infinite number of work contributions by hand would take us forever, longer than a semester.So we add them up via an integration, which allows us to do all this in minutes (much less than a semester).
Force →F=(3x2N)ˆi+(4N)ˆj, with x in meters, acts on a particle, changing only the kinetic energy of th particle. How much work is done on the particle as it moves from coordinates (2 , 3 m) to 3 m, 0 m)? Does the speed of the particle increase, decrease, or remain the same?
View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
For which of the following collisions, the external force acting on the system during collision is not appreciable as mentioned in paragraph 1.
View Solution
Knowledge Check
Collision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
For which of the following collisions, the external force acting on the system during collision is not appreciable as mentioned in paragraph 1.AA ball striking a rigid thrown wall ( consider ball as system ).BA 5 kg mass thrown vertically up exploding during its motion ( 5 kg mass is to system ).CA particle hitting a rigid bar of length L lying on frictionless surface ( consider ridig bar as the system ) .DTwo particles moving towards each other due to gravitational attraction and hitting each other ( consider any particle as system ).Collision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
According to the definition of oblique collision in the paragraph, which of the following collisions cannot be oblique'?ACollision between two point masses.BCollision between two rings of same radius.CCollision between two rings of different radius.DCollision between a particle and a ring of finite radius.Collision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
According to the definition of collision in paragraph I, which of the following physical process is not a collision?AA projectile exploding into three fragments at its highest point.BTwo soap bubbles coalescing to form a bubble of large radius.CA vertically upward thrown particle changing direction at its highest point.DA piece of magnet thrown on a metallic surface.
Collision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
According to the definition of collision in paragraph I, which of the following physical process is not a collision?
View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
Which of the following collisions is one-dimensional?
View SolutionCollision is a physical process in which two or more objects, either particle masses or rigid bodies, experience very high force of interaction for a very small duration. It is not essential for the objects to physically touch each other for collision to occur. Irrespective of the nature of interactive force and the nature of colliding bodies, Newton's second law holds good on the system. Hence, momentum of the system before and after the collision remains conserved if no appreciable external force acts on the system during collision.
The amount of energy loss during collision, if at all, is indeed dependent on the nature of colliding objects. The energy loss is observed to be maximum when objects stick together after collision. The terminology is to define collision as 'elastic' if no energy loss takes place and to define collision as 'plastic' for maximum energy loss. The behaviour of system after collision depends on the position of colliding objects as well. A unidirectional motion of colliding objects before collision can turn into two dimensional after collision if the line joining the centre of mass of the two colliding objects is not parallel to the direction of velocity of each particle before collision. Such type of collision is referred to as oblique collision which may be either two or three dimensional.
A 4kg sphere moving with a velocity of 4m/s collides with an identical sphere of 2kg moving with 2m/s as shown. Final kinetic energy is less than initial kinetic energy. What type of collision is this?
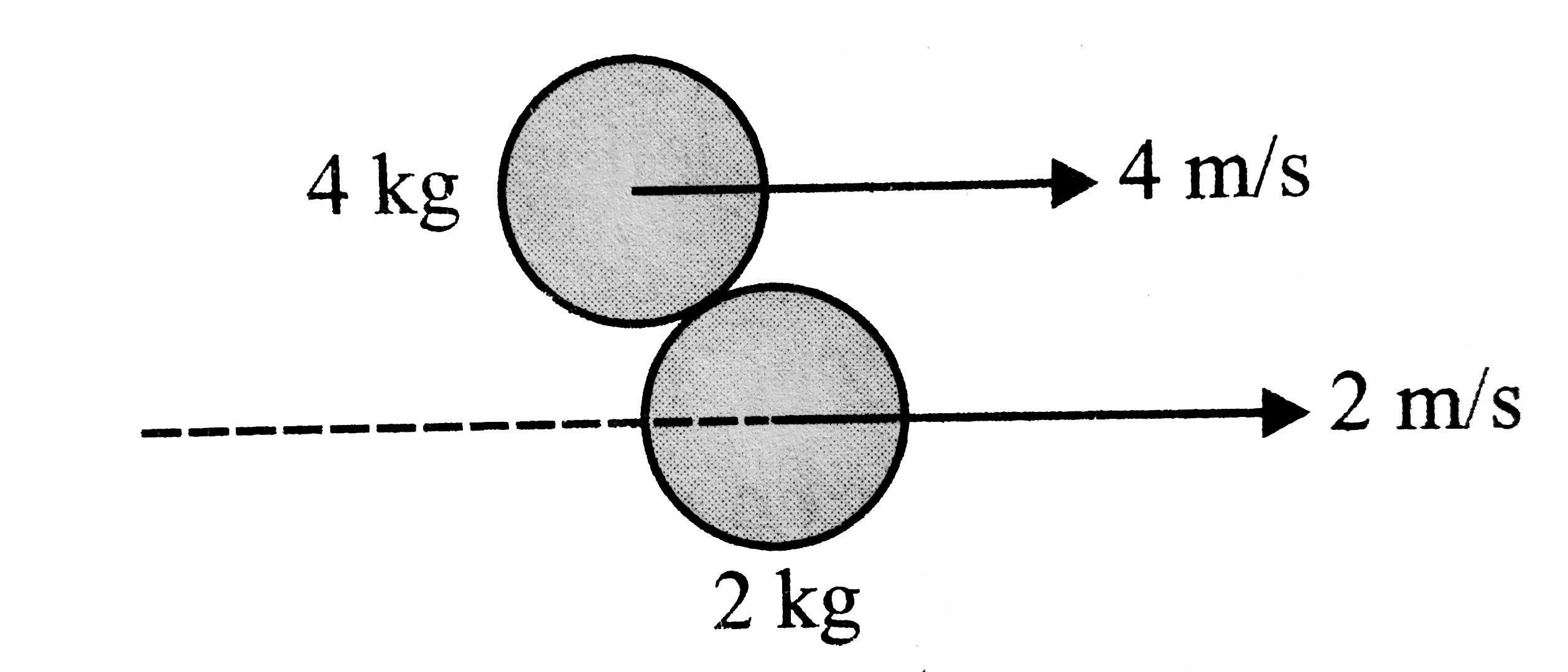
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends on the properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
Which object would first acquire half of their respective terminal speed in minimum time from start of the motion of all were released simultaneously ?
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
Which object has greatest terminal speed in the liquid ?
View Solution
