Two balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v1 towards ball 2. All collisions are assumed to be elastic. If M<m, the number of collisions between the balls will be.

Step by step video & image solution for Two balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v_(1) towards ball 2. All collisions are assumed to be elastic. If Mltm, the number of collisions between the balls will be. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Practive Exercise
28 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Discussio Q
28 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
Three balls A,B and C of same mass m are placed on a frictionless horizontal plane in a straight line as shown. Ball A is moved with velocity u towards the middle ball B. If all the collisions are elastic, find the final velocities of all the balls.

View SolutionThree balls A, B and C are placed on a smooth horizontal surface. Given that mA=mC=4mB. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collisions between the balls. All collisions are elastic.
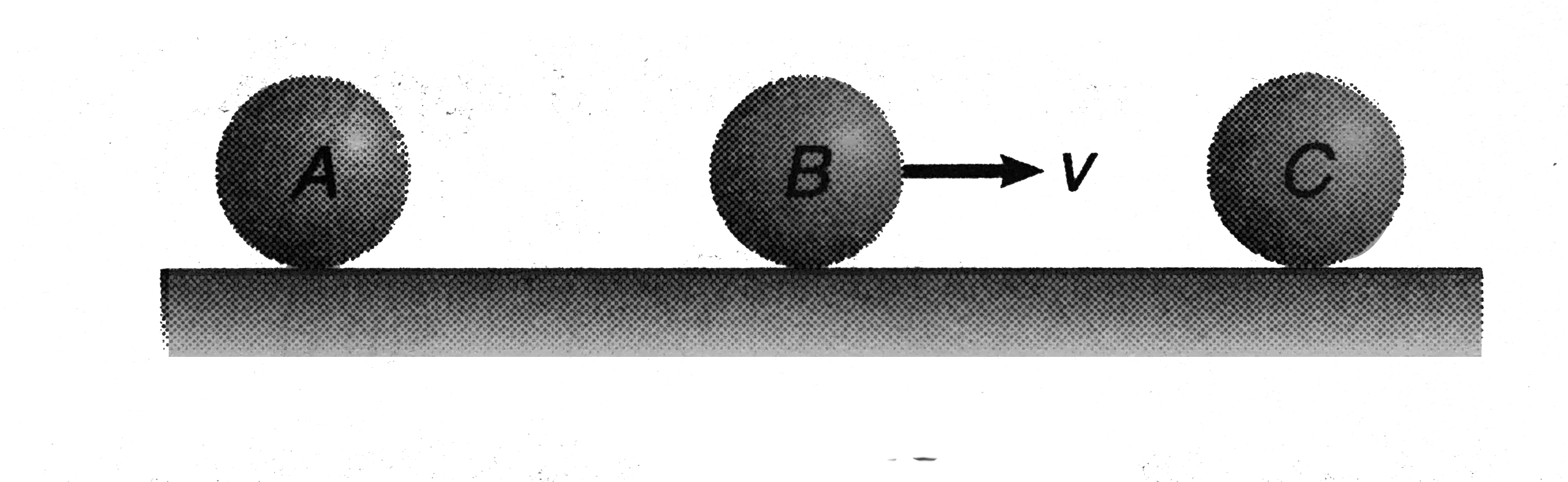
View Solution
Knowledge Check
Two balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinityTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinityA ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,
 ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
Three balls A,B and C(mA=mC=4mB) are placed onn a smooth horizontal surface. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collision betwenent the balls (all collisions are elastic).
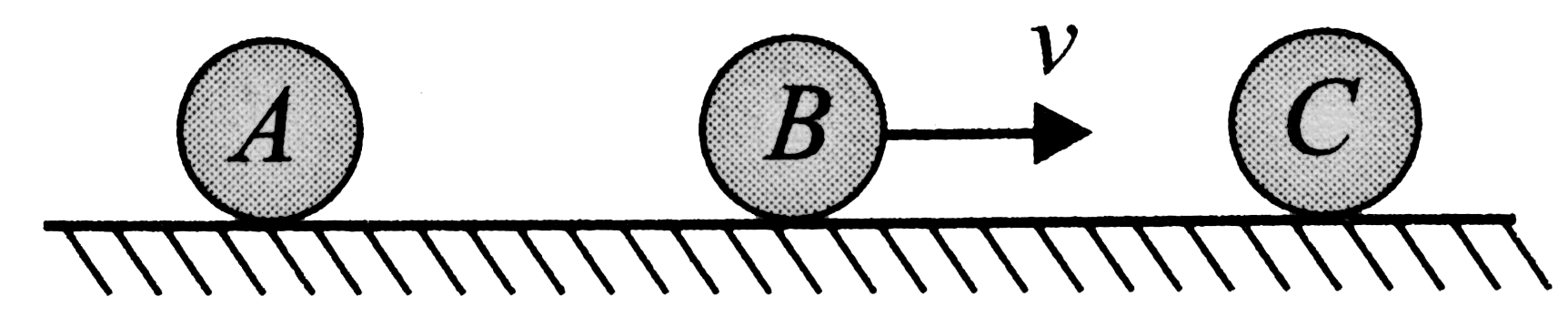
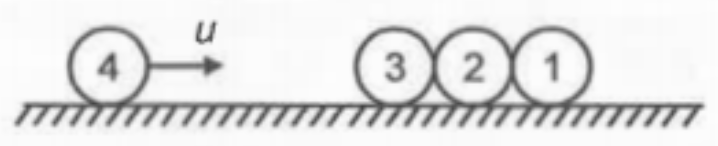
View SolutionThree identical balls 1, 2 and 3 are placed together at rest on a smooth horizontal surface. A fourth identical ball moving with velocity u in line of first three balls collides head on elastically as shown in figure, then
View SolutionTwo balls A and B each of mass m are placed on a smooth ground as shown in the figure. Another ball C of mass M arranged to the right of ball B as shown. If a velocity v1 is given to ball A in rightward direction, consider two cases. Case-I M>m and case-II M<m. Take all the collisions perfectly elastic (e=1), find the number of collision in case-I and case-II.
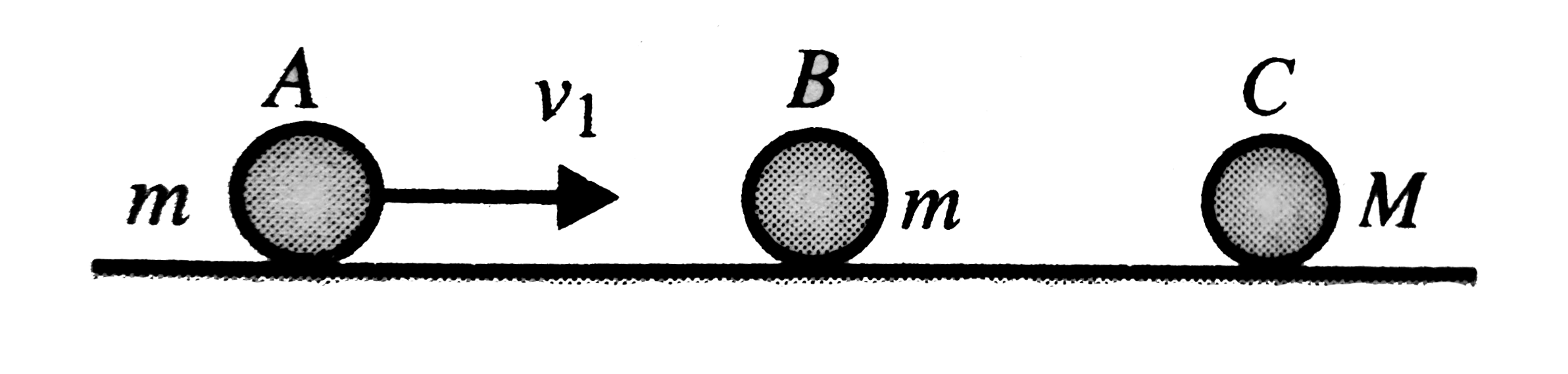
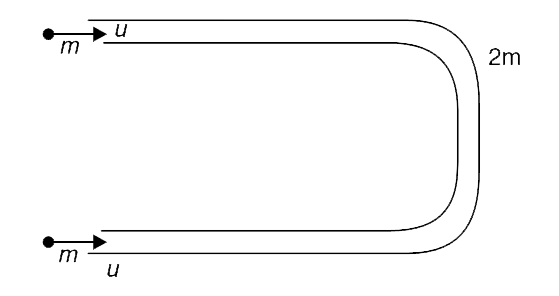
View SolutionA smooth hollow U shaped tube of mass 2m is lying at rest on a smooth horizontal table. Two small balls of mass m, moving with velocity u enter the tube simultaneously in symmetrical fashion. Assume all collisions to be elastic. Find the final velocity of the balls and the tube.
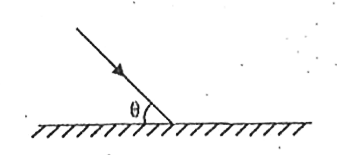
View SolutionA ball of mass m moving with speed u collides with a smooth horizontal surface at angle θ with it as shown in figure. The magnitude of impulse imparted to surface by ball is [Coefficient of restitution of collision is e]
View Solution
