A 10-kg block is placed on a horizontal surface. The coefficient of friction between them is 0.2. A horizontal force P = 15 N first acts on it in the eastward direction. Later, in addition to P a second horizontal force Q = 20 N acts on it in the northward direction.
The block will not move when only P acts, but will move when P and Q act.
If the block moves, its acceleration will be 0.5m/s2.
When the block moves, its direction of motion will be tan−1(4/3) east of north.
When both P and Q act, the direction of the force of friction acting on the block will be tan−1(3/4) west of south.
The correct Answer is:A, B, D
To solve the problem step-by-step, we will analyze the forces acting on the block and determine whether it moves or not, as well as calculate its acceleration if it does move.
Step 1: Identify the forces acting on the block
- The block has a mass m=10kg.
- The coefficient of friction μ=0.2.
- A horizontal force P=15N acts eastward.
- A second horizontal force Q=20N acts northward.
Step 2: Calculate the weight of the block
The weight W of the block is given by:
W=m⋅g
where g≈9.8m/s2.
W=10kg⋅9.8m/s2=98N
Step 3: Calculate the maximum static friction
The maximum static friction fmax can be calculated using:
fmax=μ⋅W
fmax=0.2⋅98N=19.6N
Step 4: Analyze the forces when only force P is acting
When only force P is acting:
- The applied force P=15N (eastward).
- The maximum static friction fmax=19.6N.
Since P<fmax, the block does not move when only force P is applied.
Step 5: Analyze the forces when both forces P and Q are acting
Now, consider both forces P and Q:
- The resultant force R can be calculated using the Pythagorean theorem since they are perpendicular:
R=√P2+Q2=√(15N)2+(20N)2=√225+400=√625=25N
Step 6: Determine if the block moves with both forces
Now compare the resultant force R with the maximum static friction:
- Resultant force R=25N
- Maximum static friction fmax=19.6N
Since R>fmax, the block will move when both forces are applied.
Step 7: Calculate the acceleration of the block
Using Newton's second law:
Fnet=m⋅a
The net force acting on the block when it moves is:
Fnet=R−fmax=25N−19.6N=5.4N
Now, we can find the acceleration a:
5.4N=10kg⋅a⟹a=5.4N10kg=0.54m/s2
Step 8: Determine the direction of motion
The direction of motion can be determined using the angle θ:
tan(θ)=QP=2015=43
Thus, the angle θ can be found using:
θ=tan−1(43)
Summary of Results
1. The block does not move when only force P is applied.
2. The block moves when both forces P and Q are applied.
3. The acceleration of the block is 0.54m/s2.
4. The direction of motion is given by tan−1(4/3).
- The block has a mass m=10kg.
- The coefficient of friction μ=0.2.
- A horizontal force P=15N acts eastward.
- A second horizontal force Q=20N acts northward.
The weight W of the block is given by:
W=m⋅g
where g≈9.8m/s2.
W=10kg⋅9.8m/s2=98N
The maximum static friction fmax can be calculated using:
fmax=μ⋅W
fmax=0.2⋅98N=19.6N
When only force P is acting:
- The applied force P=15N (eastward).
- The maximum static friction fmax=19.6N.
Now, consider both forces P and Q:
- The resultant force R can be calculated using the Pythagorean theorem since they are perpendicular:
R=√P2+Q2=√(15N)2+(20N)2=√225+400=√625=25N
Now compare the resultant force R with the maximum static friction:
- Resultant force R=25N
- Maximum static friction fmax=19.6N
Using Newton's second law:
Fnet=m⋅a
The net force acting on the block when it moves is:
Fnet=R−fmax=25N−19.6N=5.4N
Now, we can find the acceleration a:
5.4N=10kg⋅a⟹a=5.4N10kg=0.54m/s2
The direction of motion can be determined using the angle θ:
tan(θ)=QP=2015=43
Thus, the angle θ can be found using:
θ=tan−1(43)
1. The block does not move when only force P is applied.
2. The block moves when both forces P and Q are applied.
3. The acceleration of the block is 0.54m/s2.
4. The direction of motion is given by tan−1(4/3).
Topper's Solved these Questions
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Type 2
22 Videos
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Revision Exercise
26 Videos
- IIT QUESTIONS 5BOOK - D MUKHERJEECHAPTER - IIT QUESTIONS 5EXERCISE - Matrix matching type
2 Videos
- MISCELLANEOUS QUESTION 1BOOK - D MUKHERJEECHAPTER - MISCELLANEOUS QUESTION 1EXERCISE - Miscellaneous Questions-1 (Straight-Objective Type)
54 Videos
Similar Questions
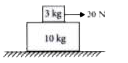
A 3kg block is placed over a 10kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.2. IF a horizontal force of 20N is applied to 3kg block. Find the acceleration of the two blocks.
View SolutionA heavy box of mass 20 kg is pulled on a horizontal force.If the coefficient of kinetic friction between the box and the horizontal surface is 0.25, find the force of friction exerted by horizontal surface on the box.
View Solution
Knowledge Check
A 10 kg block is placed on a horizontal surface whose coefficient of friction is 0.2.A horizontal force P = 15 N first acts on it in the eastward direction. Later, in addition to P a second horizontal force Q = 20 N acts on it in the northward direction: (Take g=10ms2)
AThe block will not move when only P acts, but will move when both P and Q act.BIf the block moves,the acceleration will be 0.5ms2.CWhen the block moves, its direction of motion will be tan−1(34) east of northDWhen both P and Q act, the direction of the force of friction acting on the block will be tan−1(34) west of southA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
A0.5m/s2B5m/s2C10m/s2D15m/s2A block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
A heavy box of mass 20 kg is placed on a horizontal surface . If coefficient of kinetic friction between the box and the horizontal surface . Is 0.25 calculate the force of kinetic friction Also calculate acceleration produced under a force of 98 N applied horizontally ?
View SolutionA rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30∘ with the horizontal plane , what is the force of friction on the block ? (Take g = 10m/s2)
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionA block of 5 kg is resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.2. What is the acceleration with which the block will remove if a force of 9.8 N is applied to it ?
View Solution
