While dealing with collision between particles, you must have deal from and Inertial reference frame Often we choose that frame to be fixed in the Laboratary in which the collision is observed. So it is called the Laboratary reference frame or Lab frame From Lab frame we define an elastic collision as a collision in which KE before and after collision is conserved and a perfectly inelastic collision as a collision in which after collision the two colliding bodies have same velocity vector along the line of action of impulse during collision.
If we discusss the head-on collsion between two particles from center of mass reference frame, then the velocity of center of mass (CM) will be taken to be zero in any type of collision i.e. velocity of CM before and after collision will both be zero. Since before collsion velocity of CM was zero (as our frame is fixed to CM) and no external impulse acts, it will remain zero forever
Two particles of mass 2 kg and 1kg as shown in the figure make a perfectly inelastic collision. Then if we are dealing with center of mass reference frame, the velocity of B before collision is:
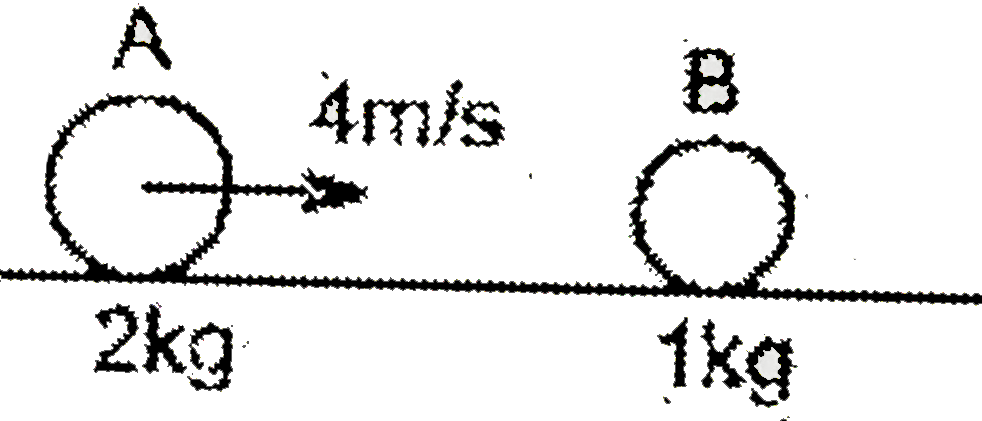
zero
8 m/s leftwards
4 m/s rightwards
83 m/s leftwards
Step by step video & image solution for While dealing with collision between particles, you must have deal from and Inertial reference frame Often we choose that frame to be fixed in the Laboratary in which the collision is observed. So it is called the Laboratary reference frame or Lab frame From Lab frame we define an elastic collision as a collision in which KE before and after collision is conserved and a perfectly inelastic collision as a collision in which after collision the two colliding bodies have same velocity vector along the line of action of impulse during collision. If we discusss the head-on collsion between two particles from center of mass reference frame, then the velocity of center of mass (CM) will be taken to be zero in any type of collision i.e. velocity of CM before and after collision will both be zero. Since before collsion velocity of CM was zero (as our frame is fixed to CM) and no external impulse acts, it will remain zero forever Two particles of mass 2 kg and 1kg as shown in the figure make a perfectly inelastic collision. Then if we are dealing with center of mass reference frame, the velocity of B before collision is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - P-2
9 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - P-3
6 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-2
21 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN
12 Videos
Similar Questions
While dealing with collision between particles, you must have deal from and Inertial reference frame Often we choose that frame to be fixed in the Laboratary in which the collision is observed. So it is called the Laboratary reference frame or Lab frame From Lab frame we define an elastic collision as a collision in which KE before and after collision is conserved and a perfectly inelastic collision as a collision in which after collision the two colliding bodies have same velocity vector along the line of action of impulse during collision.
If we discusss the head-on collsion between two particles from center of mass reference frame, then the velocity of center of mass (CM) will be taken to be zero in any type of collision i.e. velocity of CM before and after collision will both be zero. Since before collsion velocity of CM was zero (as our frame is fixed to CM) and no external impulse acts, it will remain zero forever
From CM frame, after a head-on elastic collision:
View SolutionWhile dealing with collision between particles, you must have deal from and Inertial reference frame Often we choose that frame to be fixed in the Laboratary in which the collision is observed. So it is called the Laboratary reference frame or Lab frame From Lab frame we define an elastic collision as a collision in which KE before and after collision is conserved and a perfectly inelastic collision as a collision in which after collision the two colliding bodies have same velocity vector along the line of action of impulse during collision.
If we discusss the head-on collsion between two particles from center of mass reference frame, then the velocity of center of mass (CM) will be taken to be zero in any type of collision i.e. velocity of CM before and after collision will both be zero. Since before collsion velocity of CM was zero (as our frame is fixed to CM) and no external impulse acts, it will remain zero forever
From CM frame, after a perfectly inelastic head-on collision:
View Solution
Knowledge Check
In perfectly inelastic collision
AOnly momentum is conservedBMomentum and total energy both are conserved,CMomentum 'and kinetic energy both are conservedDOnly kinetic energy is conserved.In perfectly elastic collision
AOnly momentum is conservedBMomentum and kinetic energy both are conservedCNeither momentum nor kinetic energy is conservedDOnly kinetic energy is conserved.For perfectly elastic collision
Av2−v1=u2−u1Bv1−v2=u1−u2Cv2−v1=u1−u2Dv2−v1=u1+u22
While dealing with collision between particles, you must have deal from and Inertial reference frame Often we choose that frame to be fixed in the Laboratary in which the collision is observed. So it is called the Laboratary reference frame or Lab frame From Lab frame we define an elastic collision as a collision in which KE before and after collision is conserved and a perfectly inelastic collision as a collision in which after collision the two colliding bodies have same velocity vector along the line of action of impulse during collision.
If we discusss the head-on collsion between two particles from center of mass reference frame, then the velocity of center of mass (CM) will be taken to be zero in any type of collision i.e. velocity of CM before and after collision will both be zero. Since before collsion velocity of CM was zero (as our frame is fixed to CM) and no external impulse acts, it will remain zero forever
After collision, the velocity of B in CM reference frame will be
View SolutionWhile dealing with collision between particles, you must have deal from and Inertial reference frame Often we choose that frame to be fixed in the Laboratary in which the collision is observed. So it is called the Laboratary reference frame or Lab frame From Lab frame we define an elastic collision as a collision in which KE before and after collision is conserved and a perfectly inelastic collision as a collision in which after collision the two colliding bodies have same velocity vector along the line of action of impulse during collision.
If we discusss the head-on collsion between two particles from center of mass reference frame, then the velocity of center of mass (CM) will be taken to be zero in any type of collision i.e. velocity of CM before and after collision will both be zero. Since before collsion velocity of CM was zero (as our frame is fixed to CM) and no external impulse acts, it will remain zero forever
If collision were elastic in above question then velocity of B after collision in CM reference frame will be:
View SolutionReference Frame
View SolutionAfter perfect inelastic collision
View SolutionIn an elastic collision between two particles
View Solution
