A sphere moving with velocityv strikes elastically with a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large, the work done by the wall during collision wiHbe:
mu (u+υ)
2mu(u+υ)
2mυ(u+υ)
2m(u+υ)
The correct Answer is:B
Step by step video, text & image solution for A sphere moving with velocityv strikes elastically with a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large, the work done by the wall during collision wiHbe: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-2
21 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-3,(P-1)
5 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example
50 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN
12 Videos
Similar Questions
A ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
View SolutionA ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
View Solution
Knowledge Check
A Sphere moving with velocity v strikes a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large the work done by the wall during collision will be:
Amu(v+u)B2mu(v+u)C2mv(v+u)D2m(v+u)A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
AThe average elastic force acting on the ball is [m(u+v)]/△tBThe average elastic force acting on the ball is [2m(u+v)]/△tCThe kinetic energy of the ball increases by 2mu(u+v).DThe kinetic energy of the ball remains the same after the collision.A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
AThe average elastic force acting on the ball is m(u+v)ΔtBThe average elastic force acting on the ball is 2m(u+v)ΔtCthe kinetic energy of the ball increases by 2mu (u + v)Dthe kinetic energy of the ball does not change
A ball of mass 'm' collides with a wall with speed 'V' and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
View SolutionA ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If mass of the wall is taken as infinite, then the work done by the ball on the wall is
View SolutionA wall moving with velocity 2cms−1 towards the ball and ball is moving towards the wall with a velocity 10cms−1. It hits the wall normally and makes elastic collision with wall. The velocity of ball after collision with wall in cms−1.
View SolutionA molecule of mass m moving at a velocity v impinges elastically on the wall at an angle a with the wall. Then
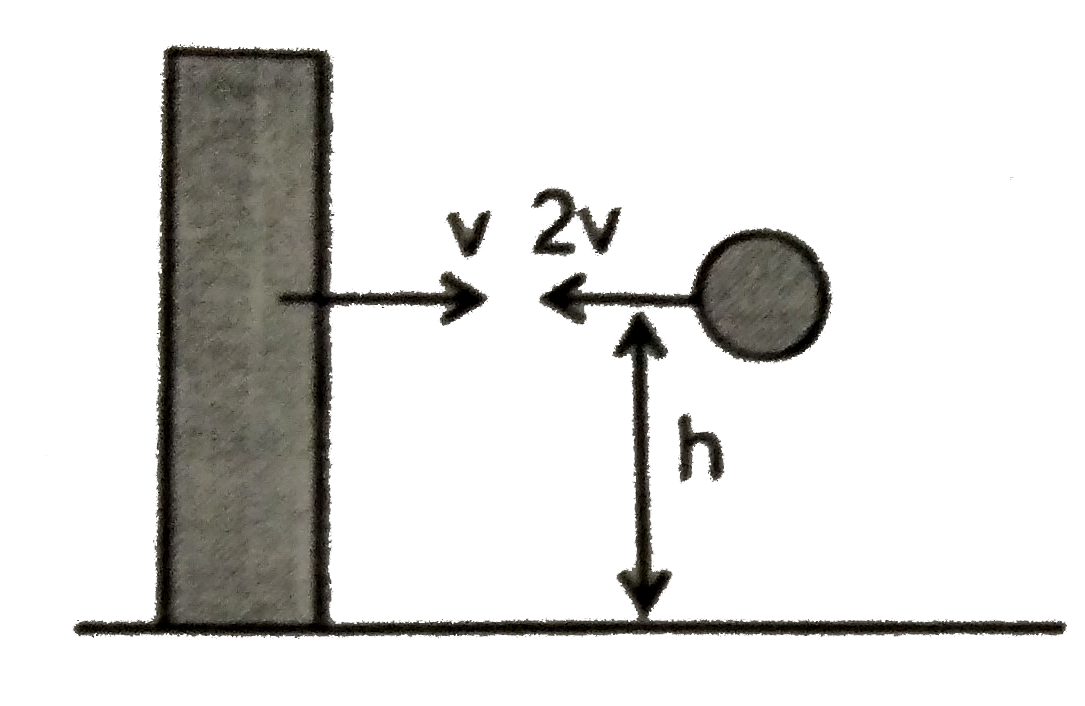
View SolutionA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
View Solution
