A rectangular block is composed of three different glass prisms (with refractive indices μ1,μ2 and μ3) as shown in the figure below. A ray of light incident normal to the left face emerges normal to the right face. Then the refractive indices are related by

μ21+μ22=2μ23
μ21+μ22=μ23
μ21+μ23=2μ22
μ22+μ23=2μ21
The correct Answer is:C
Step by step video, text & image solution for A rectangular block is composed of three different glass prisms (with refractive indices mu_(1), mu_(2) and mu_(3)) as shown in the figure below. A ray of light incident normal to the left face emerges normal to the right face. Then the refractive indices are related by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
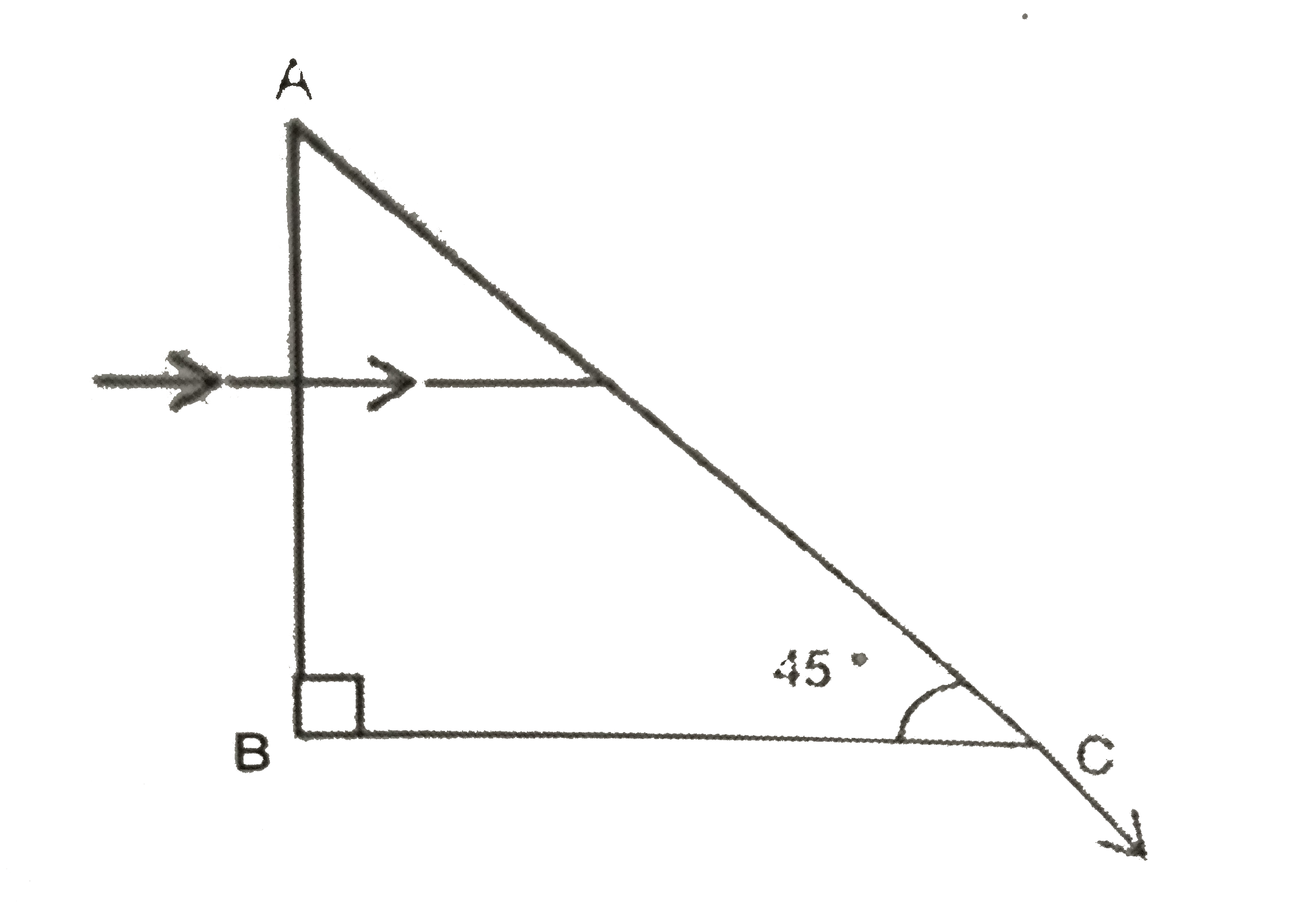
What is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
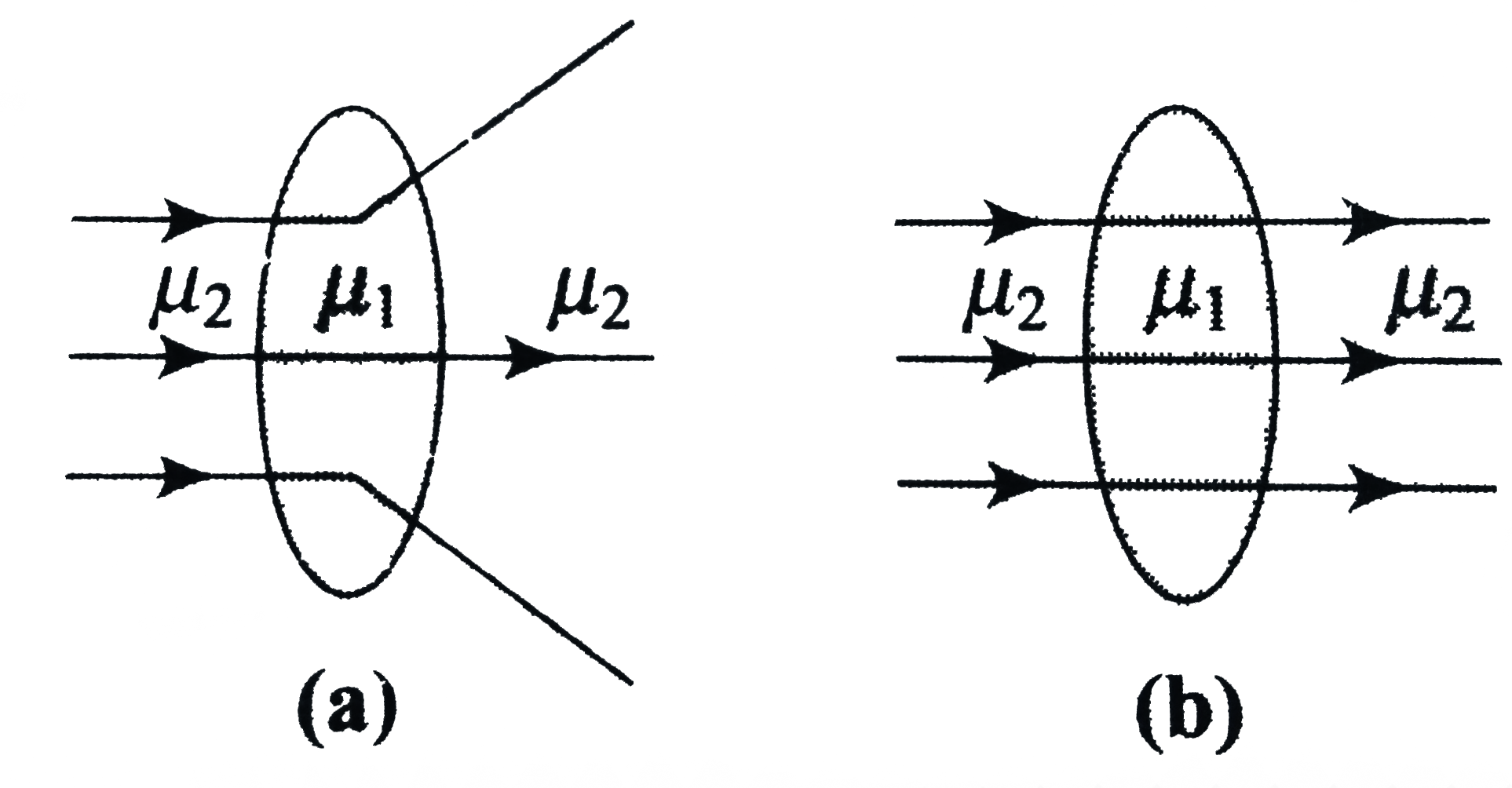
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
View Solution
Knowledge Check
A ray of light passes through four transpar ent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in figure. The surfaces of all media are parallel. If the emergent ray is parallel to the incident ray, we must hav
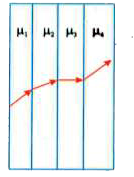 Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1
Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1A ray of light passes through four transparent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in the figure. The surfaces of all media are parallel. If the emergent ray CD is parallel to the incident ray AB, we must have
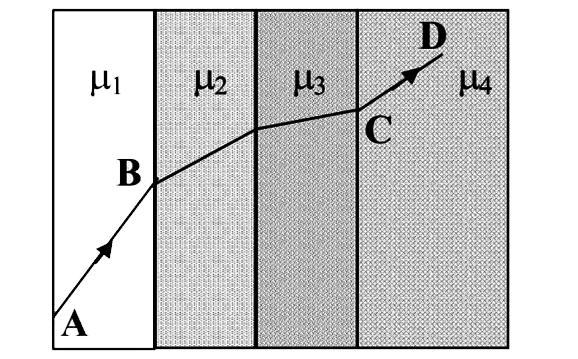 Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1
Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1A ray of light passes through four transparent media with refractive indices μ1,μ2,μ3,andμ4 as shown in figure. The surfaces of all media are paralle. If the emerent ray CD is parallel to the incident ray AB, we must have
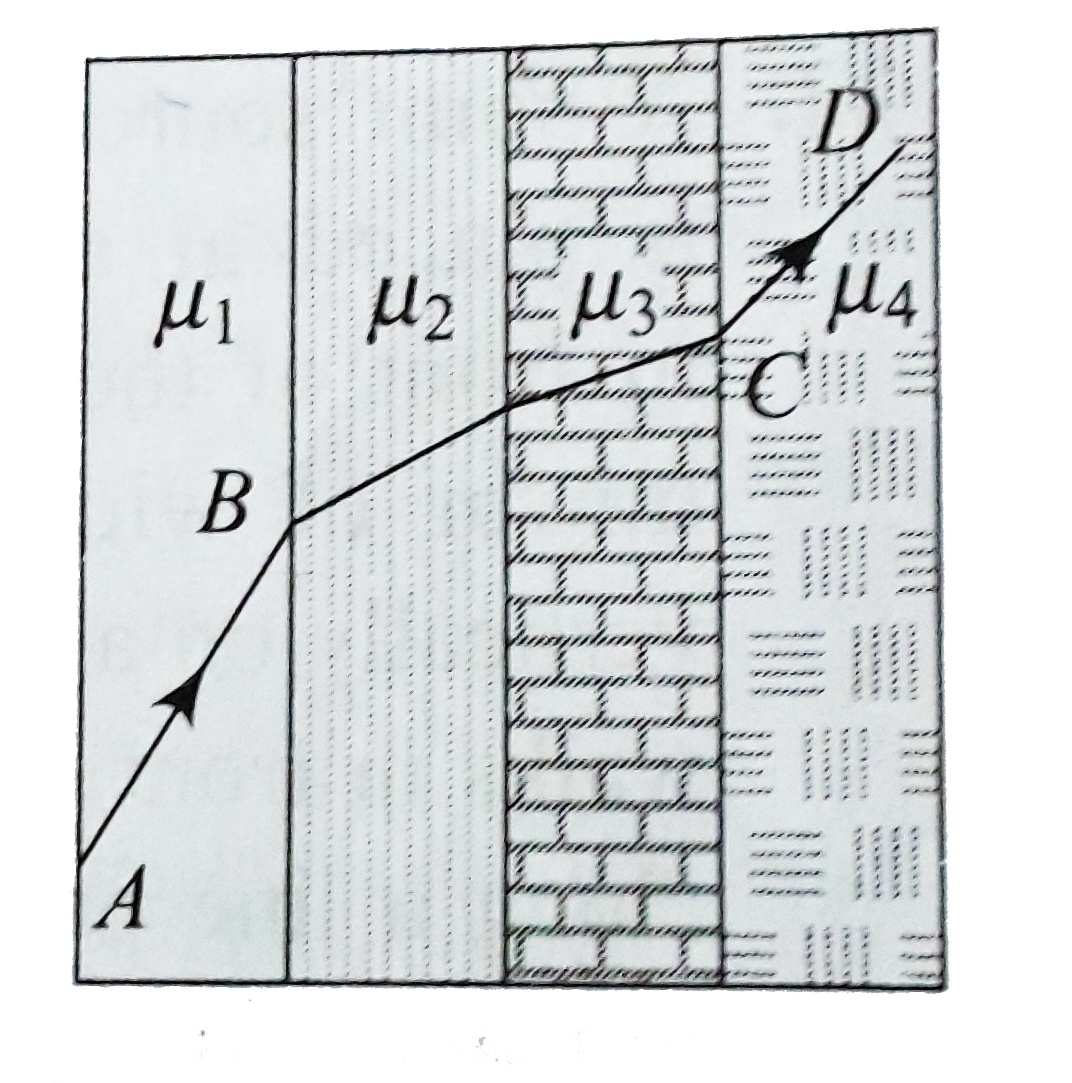 Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1
Aμ1=μ2Bμ2=μ3Cμ3=μ4Dμ4=μ1
In the figure given below, a ray of light PQ is incident normally on one face AB of an equilateral glass prism. What are the angles at faces AB and AC?

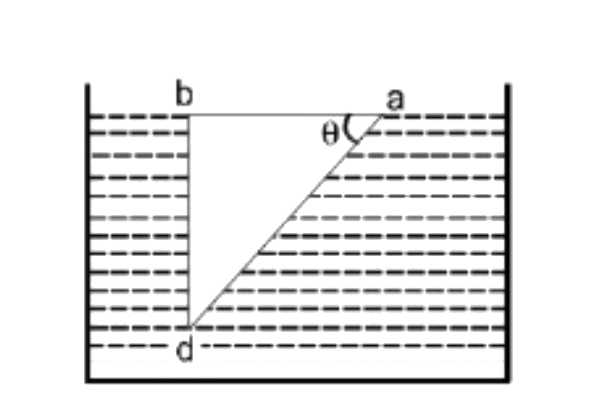
View SolutionA glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
View SolutionThree transparent media of refractive indices μ1,μ2,μ(3) respectively, are stacked as shown. A ray of light follows the path shown. No light enters the third medium.

Then-
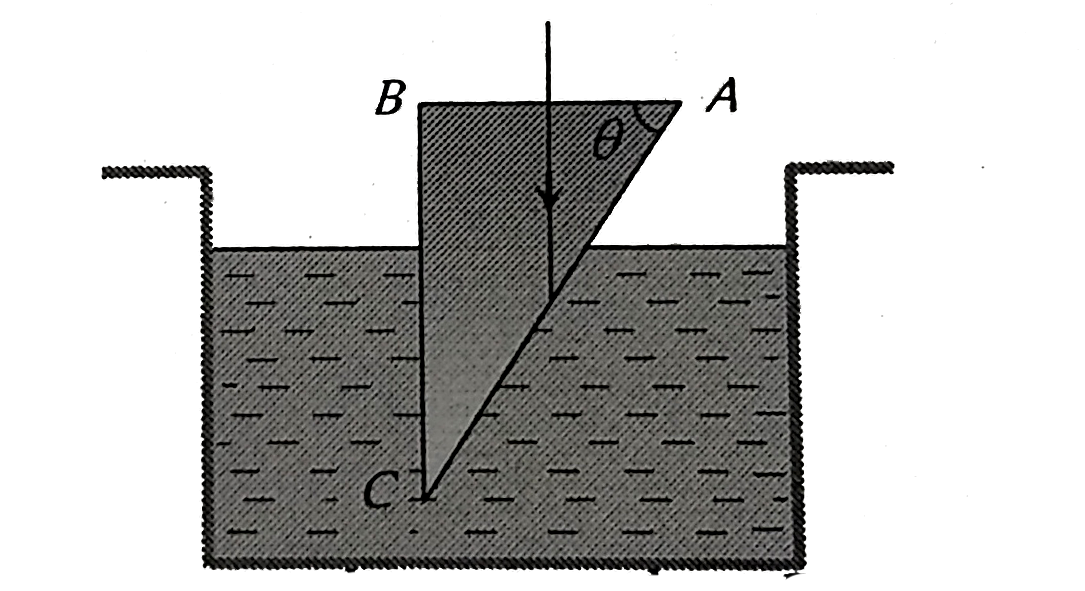
View SolutionA glass prism (μ=1.5) is dipped in water (μ=4/3) as shown in figure. A light ray is incident normally on the surface AB . It reaches the surface BC after totally reflected, if
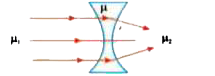
View SolutionThe relation between refractive indices u,μ1,μ2. if the behaviour of light ray is as shown in figure
View Solution

