A cylinder of weight W and radius R is to be raised onto a horizontal step of height h as shown in Fig. A rope is wrapped around the cylinder and pulled horizontally with force F. Assuming the cylinder does not slip on the step, find the minimum force F necessary to raise the cylinder.
Step by step video & image solution for A cylinder of weight W and radius R is to be raised onto a horizontal step of height h as shown in Fig. A rope is wrapped around the cylinder and pulled horizontally with force F. Assuming the cylinder does not slip on the step, find the minimum force F necessary to raise the cylinder. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE83videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
A cylinder of weight W and raidus R is to be raised onto a horizontal step of height h=R/3 as shown. A rope is wrapped around the cylinder and pulled horizontally. Assuming no slipping, find the minimum value of F to raise the cylinder.
View SolutionA uniform cylinder of mass M and radius R is to be pulled over a step of height a (a<R) by applying a force F at its centre O perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure ) . The minimum value of F required is :
View Solution
Knowledge Check
- Question 1 - Select One
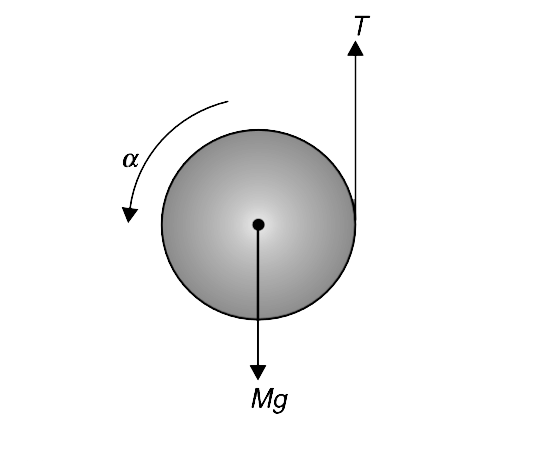
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
AmgM+mB2mgM+mC2mgM+2mD2mg2M+m - Question 2 - Select One
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3m - Question 3 - Select One
A cylinder of height H and diameter H/4 is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is 2H from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
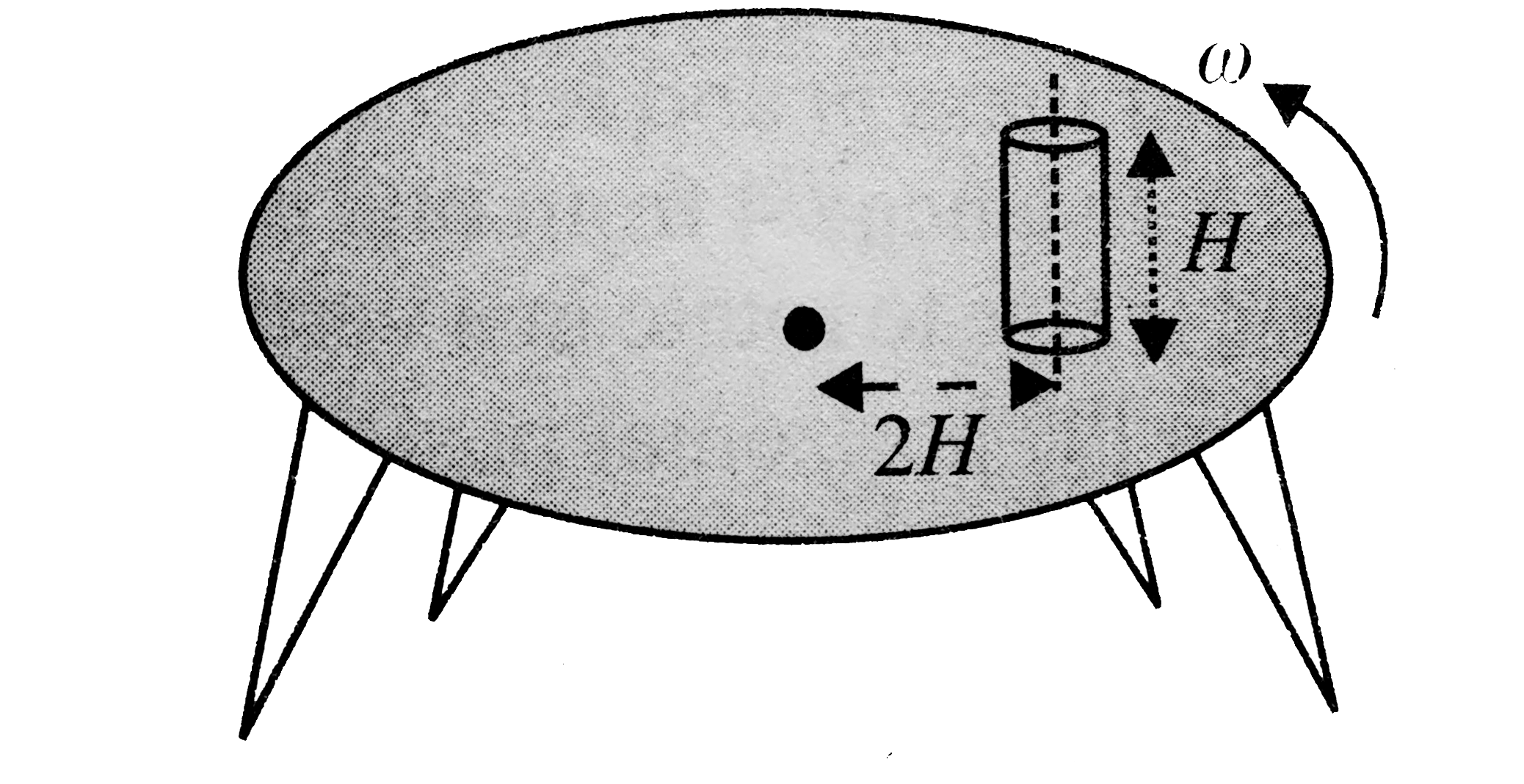A√g2(12−H)B√g(12−H)C√g4HD√g8H
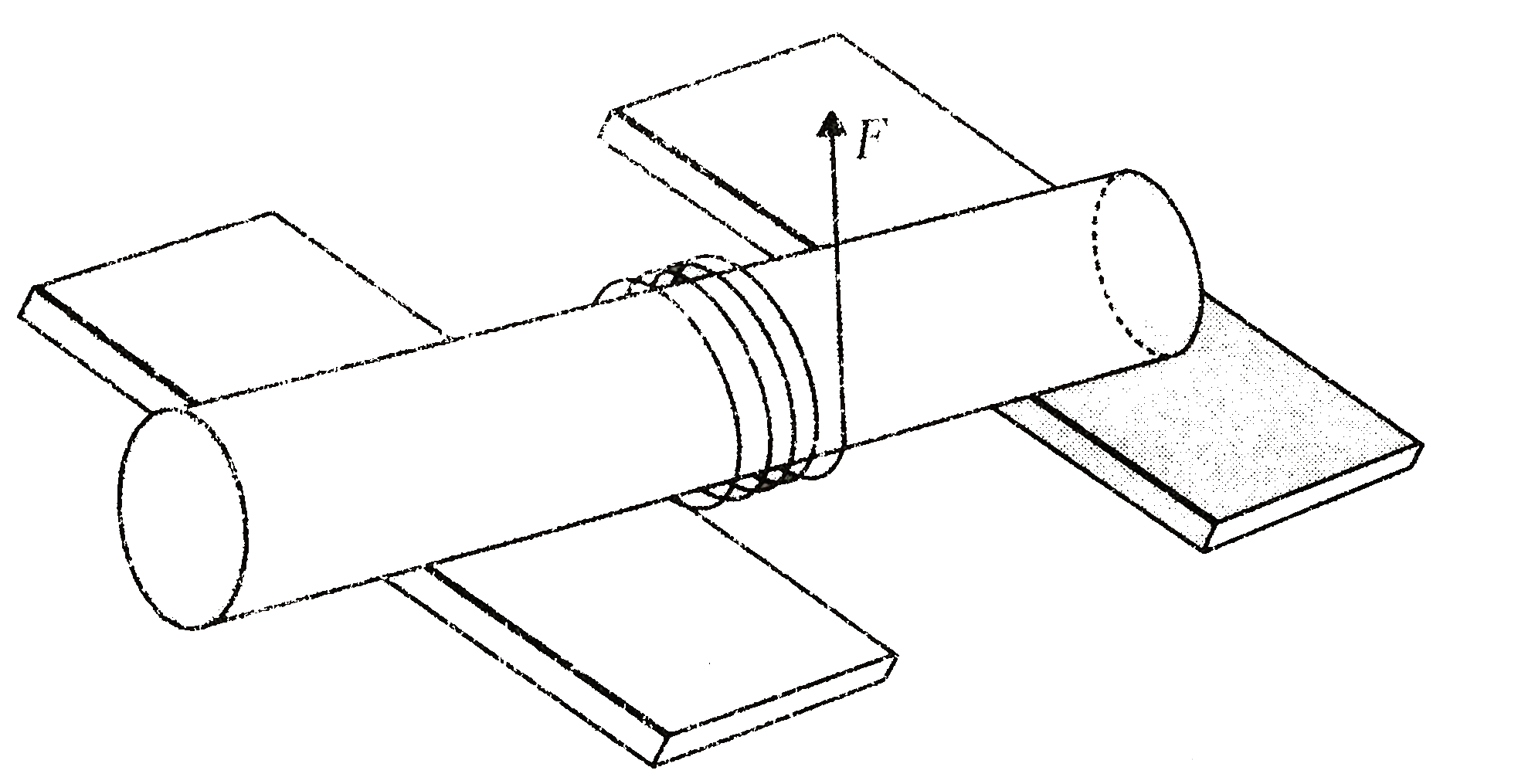
A uniform solid cylinder of mass m rests on two horizontal planks as shown in Fig. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically up with a force F. What is the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to μ. What is the maximum acceleration of the axis of the cylinder?
View SolutionA string is wrapped around a cylinder of radius R and pulled at the top most point horizontally by a force F The cylinder rolls without slipping on the horizontal surface. The work done by the force by the time the cylinder makes one full rotation is
View SolutionA string is wrapped around a cylinder of radius R and pulled at the top most point horizontally by a force F The cylinder rolls without slipping on the horizontal surface. The work done by the force by the time the cylinder makes one full rotation is WR
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed ω.
View SolutionA plank of mass M is placed on a smooth surface over which a cylinder of mass m and radius R is placed as shown in figure-5.63. Now the plank is pulled towards right with an external force F. If cylinder does not slip over the surface of plank find the linear acceleration of plank and cylinder and the angular acceleration of the cylinder.
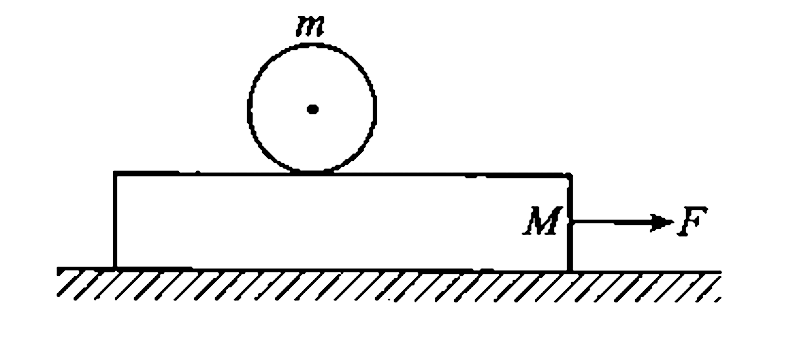
View Solution