A spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
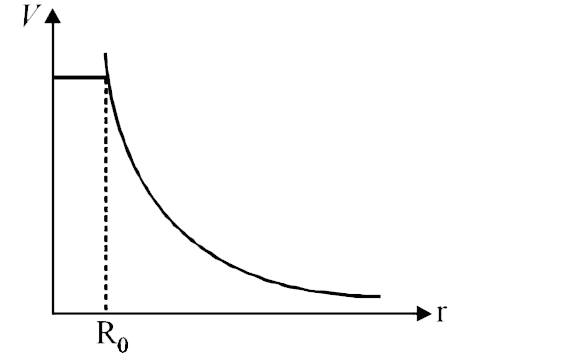
Choose the incorrect statement.
Electric field due to the charge system is discontinuous at r=ro
The net charge enclosed-in a sphere ofradi us r=2ro is Q
No charge exists at any point in a spherical region of radius r<ro
Electrostatic energy inside the sphere of radius r=ro is zero
The correct Answer is:C
Step by step video & image solution for A spherical symmetric charge system is centered at origin. Given, Electric potential V=(Q)/(4piepsilon_0R_0)(rleR_0), V=(Q)/(4piepsilon_0r)(rgtR_0) Choose the incorrect statement. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Numerical MCQs Single options Correct
64 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
Similar Questions
For spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View SolutionSix point charges are kept at the vertices of a regular hexagon of side L and centre O, as shown in the figure. Given that K=14πε0qL2, which of the following statements(s) is (are) correct?
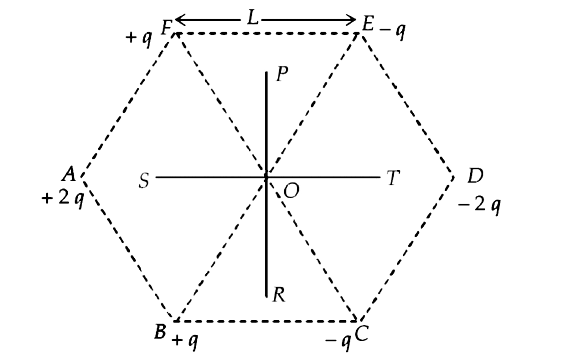
View Solution
Knowledge Check
The electrostatic potential ϕr, of a spherical symmetrical system kept at origin, is shown in the adjacent figure, and given as
ϕr=q4πε0r(r≥R0)
ϕr=q4πε0R0(r≤R0)
Which of the following option is incorrect ?
 AFor spherical region r≤R0 total electrostatic energy stored is zeroBWith in r=2R0, total charge is q/2CThere will be no charge anywhere except at r = RDElectric field is discontinuous at r=R0
AFor spherical region r≤R0 total electrostatic energy stored is zeroBWith in r=2R0, total charge is q/2CThere will be no charge anywhere except at r = RDElectric field is discontinuous at r=R0The electrostatic potential (ϕr) of a spherical symmetric system , kept at origin is shown in the adhacent figure, and given as
ϕe=q4πɛ0r(r≤Ro)
ϕe=q4πɛ0Ro(r≤R0)

Which of the following option s in //are correct ?AFor spherical region r≤R0 total electrostatic energy stored id zero .BWithin r=2R0, total charge is q.CThere will be no charge anywhere except at r=R0.DElectric field is discontinuous at r=R0.A charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
A−(4.32ˆi+5.76ˆj)×102N/CB−(4.32ˆi−5.76ˆj)×102N/CC−(5.76ˆi+4.32ˆj)×102N/CD(4.32ˆi+5.76ˆj)×102N/C
A cubical region of side a has its centre at the origin. It encloses three point charges , −q at (0,−a/4,0),+3qat(0,0,0) and −q at (0,+a/4,0).
Choose the correct option (s)

(i) The net electric flux crossing the plane x=+q2 is equal to the net electric flux crossing the plane x=−a2
(ii) The net electric flux crossing the plane y=+a2 is more than the net electric flux crossing the plane y=−a2
(iii) The net electric flux crossing the entire region is qε0
(iv) The net electric flux crossing the plane z=+a2 is equal to the net electric flux crossing the plane x=+a2
View SolutionA regular hexagon of side a has a charge Q at each vertex. Potential at the centres of hexagon is (k= (14πε0))
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ(54−rR) upto r=R, and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
View SolutionA spherical conducting shell of radius r0 carry a charge q0. Then value of electric field inside it is :-
View SolutionWithin a spherical charge distribution of charge density ρ(r), N equipotential surface of potential V0,V0+ΔV,V0+2ΔV,…V0+NΔV(ΔV>0), are drawn and have increasing radii r0,r1,r2,….RN, respectively. If the difference in the radii of the surface is constant for all values of V0 and ΔV then :-
View Solution
