A spherical tank of radius 0.35m is half filled with oil of relative density 0.8. if the tank is moving with a horizontal acceleration of 10ms2. The surface of oil is at rest with respect to sphere. The maximum gauge pressure of oil in the tank is n×103Pa, the value of n is approximately equal to (take g=10ms2
The correct Answer is:4
tan=ag=1
⇒θ=45∘
Pmax=ρghmax=ρg×√2R
≈4×103N/m2
Similar Questions
(a) A spherical tank of 1.2m radius is half filled with oil of relaive density 0.8. If the tank is given a horizontal acceleration of 10m/s2. Calculate the inclination of the oil surface to horizontal and maximum pressure on the tank.
(b) The volume of an air bubble is doubled as it rises from the bottom of a lake to its surface. If the atmospheric pressure is Hm of mercury & the density of mercury is n times that of lake water. Find the depth of the lake.
View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View Solution
Knowledge Check
A spherical tank of 1.2m radius is half filled with oil of relative density 0.8. If the tank is given a horizontal acceleration of 10m/s2, the maximum pressure on the tank is √2P pascal. Find the value of P.
A8600B9600C5800D6500The velocity of kerosene oil in a horizontal pipe is 5m/s. If g=10m/s2 then the velocity head of oil wlill be
A1.25mB12.5mC0.125mD125mWhat angle θ to the horizon will be formed by the surface of petrol in the tank of a motor car moving horizontally with a constant acceleration of 2.44 m/s2 ?
Aθ=14∘Bθ=45∘Cθ=30∘Dθ=0
A cylindrical tank having radius R is half filled with water having density ρ. There is a hole at the top of the tank. The tank is moved horizontally. Perpendiular to its length, with a constant acceleration equal to the acceleration due to gravity (g). Find the maximum pressure exerted by water at any point on the tank. Atmospheric pressure is P0. Assume that there is no spillage.
View SolutionAn iron ball of radius 0.3 cm falls through a column of oil of density 0.94 g cm−3. If it attains a terminal velocity of 0.54 m s−1, what is the viscosity of oil? Density of iron is 7.8 g cm−3
View SolutionA solid sphere of mass m=2kg and density ρ=500kg/m3 is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water=1000kg/m3,g=10m/s2)
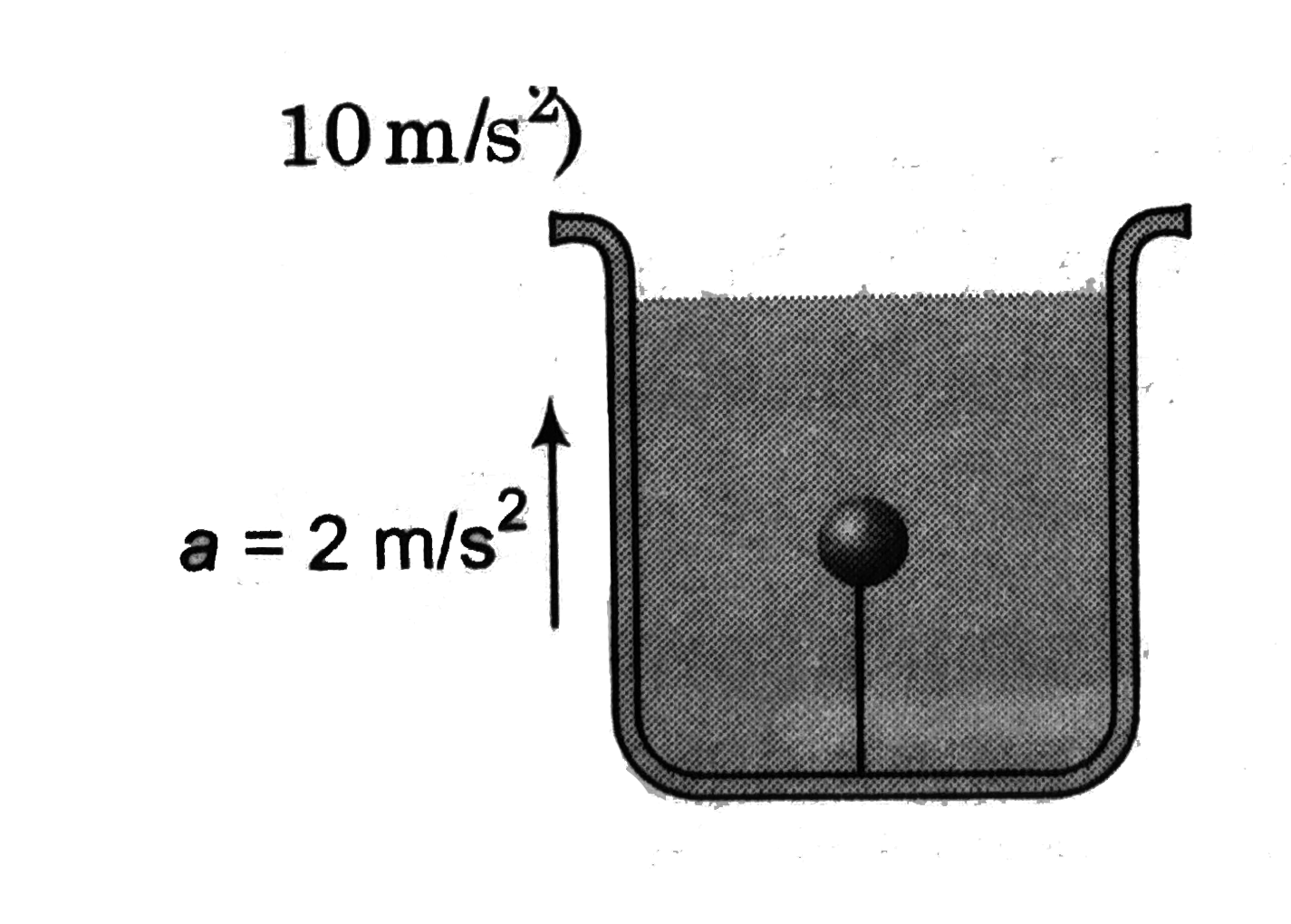
View SolutionA solid sphere of mass m=2kg and specific gravity s=0.5 is held stationary relative to a tank filled with water. The tank is accelerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank.
(Density of water =1000kgm−3,g=10ms−2).
 .
.
View SolutionA tank 5 m high is half filled with water and then is filled to the top with oil of density 0.85 g The pressure at the bottom of the tank, due to these liquids is
View Solution
