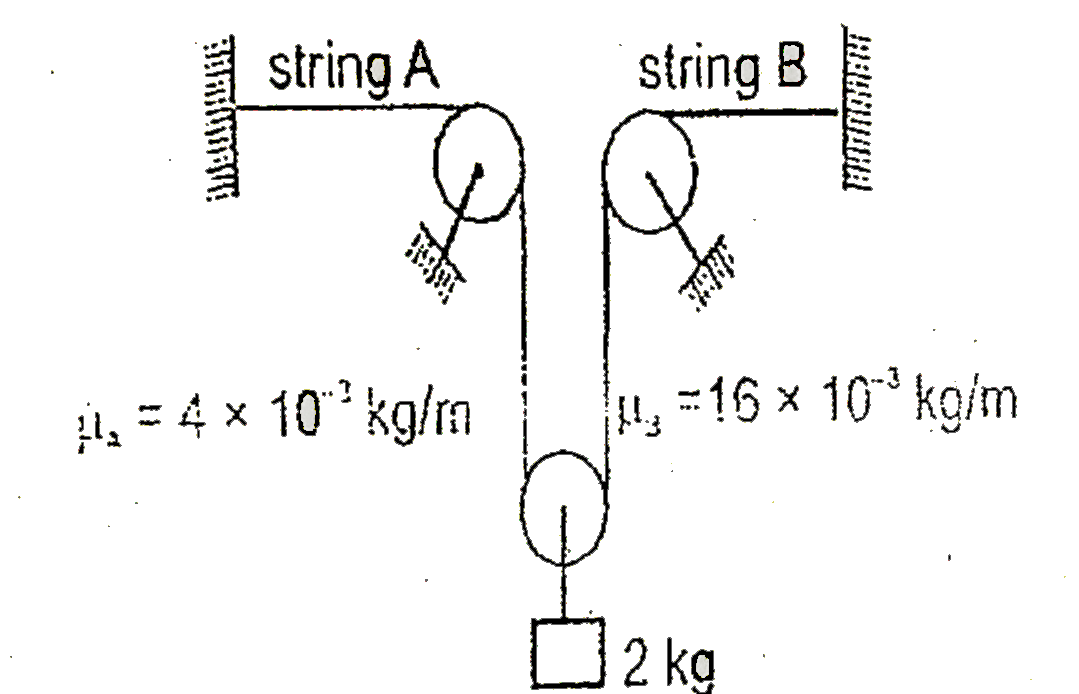Transverse waves of same frequency are generated in two steel wires A and B . The diameter of A is twice of B and the tension in A is half that in B. The ratio of velocities of wave in A and B is
1:3√2
1:2√2
1:2
√2:1
The correct Answer is:B
To solve the problem, we need to find the ratio of the velocities of waves in two steel wires A and B, given their diameters and tensions.
Step 1: Understand the relationship between wave velocity, tension, and mass per unit length.
The velocity v of a wave in a string is given by the formula:
v=√Tμ
where T is the tension in the wire and μ is the mass per unit length of the wire.
Step 2: Relate mass per unit length to diameter and density.
The mass per unit length μ can be expressed in terms of the density ρ and the diameter D of the wire:
μ=ρ⋅A=ρ⋅(πD24)
where A is the cross-sectional area of the wire.
Step 3: Set up the equations for wires A and B.
Let the diameter of wire B be D. Then the diameter of wire A is 2D. The radii are:
rA=DA2=DandrB=DB2=D2
The mass per unit length for wires A and B can be expressed as:
μA=ρ⋅(π(2D)24)=ρ⋅πD2
μB=ρ⋅(πD24)=ρ⋅πD24
Step 4: Substitute the tensions and mass per unit lengths into the velocity formula.
Given that the tension in wire A is half that in wire B:
TA=12TB
Now we can express the velocities:
vA=√TAμA=
⎷12TBρ⋅πD2
vB=√TBμB=
⎷TBρ⋅πD24
Step 5: Find the ratio of the velocities.
Now, we can find the ratio vAvB:
vAvB=√12TBρ⋅πD2√TBρ⋅πD24
This simplifies to:
vAvB=
⎷1241=√12⋅14=√18=12√2
Final Step: Express the ratio in a simpler form.
Thus, the ratio of velocities vA:vB is:
vA:vB=1:2√2
Final Answer:
The ratio of velocities of waves in A and B is 1:2√2.
The velocity v of a wave in a string is given by the formula:
v=√Tμ
where T is the tension in the wire and μ is the mass per unit length of the wire.
The mass per unit length μ can be expressed in terms of the density ρ and the diameter D of the wire:
μ=ρ⋅A=ρ⋅(πD24)
where A is the cross-sectional area of the wire.
Let the diameter of wire B be D. Then the diameter of wire A is 2D. The radii are:
rA=DA2=DandrB=DB2=D2
μA=ρ⋅(π(2D)24)=ρ⋅πD2
μB=ρ⋅(πD24)=ρ⋅πD24
Given that the tension in wire A is half that in wire B:
TA=12TB
vA=√TAμA=
⎷12TBρ⋅πD2
vB=√TBμB=
⎷TBρ⋅πD24
Now, we can find the ratio vAvB:
vAvB=√12TBρ⋅πD2√TBρ⋅πD24
This simplifies to:
vAvB=
⎷1241=√12⋅14=√18=12√2
Thus, the ratio of velocities vA:vB is:
vA:vB=1:2√2
The ratio of velocities of waves in A and B is 1:2√2.
Topper's Solved these Questions
- WAVES AND SOUNDBOOK - ERRORLESS CHAPTER - WAVES AND SOUNDEXERCISE - Organ pipe
53 Videos
- WAVES AND SOUNDBOOK - ERRORLESS CHAPTER - WAVES AND SOUNDEXERCISE - Doppler s Effect
65 Videos
- WAVES AND SOUNDBOOK - ERRORLESS CHAPTER - WAVES AND SOUNDEXERCISE - Stationary Waves
39 Videos
- VECTORSBOOK - ERRORLESS CHAPTER - VECTORSEXERCISE - Exercise
223 Videos
- WORK , ENERGY , POWER AND COLLISIONBOOK - ERRORLESS CHAPTER - WORK , ENERGY , POWER AND COLLISIONEXERCISE - Self Evaluation Test
19 Videos
Similar Questions
Knowledge Check
Transverse waves are generated in two uniform steel wires AandB by attaching their free ends to a fork of frequency 500Hz. The diameter of wire A is half that B and tension in wire A is half the tension in wire B. What is the ratio of velocities of waves in AandB?
A1:2B√2:1C2:1D1:√2The diameter of ball A is half of that of B. The ratio of their terminal velocities will be
A2:4B4:1C1:4D2:4Transverse waves are generated in two uniform wires A and B of the same material by attaching their free ends to a vibrating source of frequency 200Hz. The cross sectiona of A is half that of B while the tension on A is twice that on B. The ratio of wavelengths of transverse waves in A and B is
A1:√2B√2:1C1:2D2:1
Two strings A and B, made of the same material, have equal lengths. The cross sectional area of A is half that of B while the tension on A is twice that on B. The ratio of the velocities of transverse waves in A and B is:
View SolutionCalculate the ratio of intensity of wave train A to wave train B.
_E01_106_Q01.png)
View SolutionTransverse waves are generated in two uniform wires A and B of the same material by attaching their free ends to a vibrating source of frequency 200Hz. The cross sectional area of A is half that of B while the tension on A is twice that on B. The ratio of the wavelengths of the transverse waves in A and B is
View SolutionTwo capillaries A and B are dipped in water and held vertical . The diameter of A is twice that of B . The ratio of the heights to which water rises in A and B is
View SolutionTwo circular iron discs are of the same thickness. The diameter of A is twice of B . The moment of inertia of A as compared to that of B is
View Solution