Two particles A and B of masses 1kg and 2kg respectively are projected in the directions shown in figure with speeds uA=200m/s and uB=50m/s. Initially they were 90m apart. They collide in mid air and stick with each other. Find the maximum height attained by the centre of mass of the particles. Assume acceleration due to gravity to be constant.
(g=10m/s2)

→Psys=MT→VCM
d→Psysdt=MT→aCM
→Fext=MT→aCM
Net external force is the gravitational force
Fext=MT×g
∴ →acm=g⏐↓(dwonwards)
(→Vcm)=mA→VA+mB→VBmA+mB=1×200−2×503=1003m/s↑⏐
⏐
⏐⏐ (upwards)
initial height of centre of mass from A,h0=1×0+2×901+2=60m
hmax=inital height (h0)+v2cm2g=60+(1003)22×10=115.55m
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Solved Examples
15 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Practice Exercise
20 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
Two particles A and B of mass 1 kg and 2 kg respectively are projected in the direction shown in figure with speeds uA=200ms−1 and uB=50ms−1. Initially they were 90 m apart. Find the maximum height attained by the center of mass of the particles. Assume acceleration due to gravity to be constant. (Take, g=10ms−2.
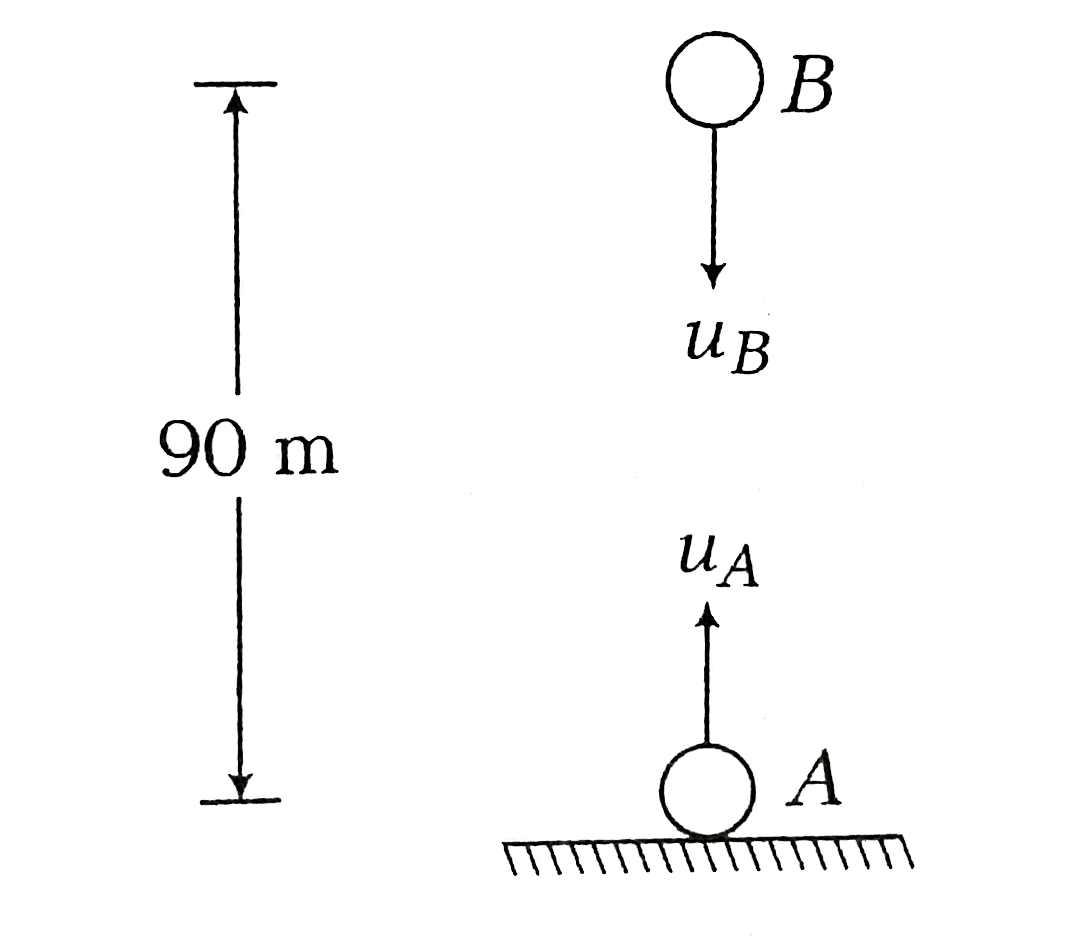
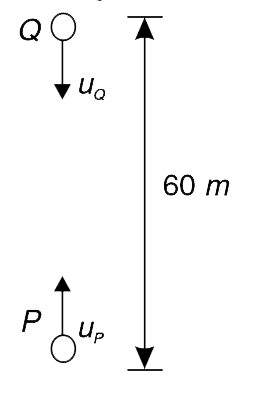
View SolutionTwo particles PandQ have mass 1kgand2kg respectively. They are projected along a vertical line with velocity up=20 m/s and uQ=5 m/s when separation between them was 60 m. P was projected vertically up while Q was projected vertically down. Calculate the maximum height attained by the centre of mass of the system of two particles, measured from the initial position of P. Assume that the particles do not collide and that the ground is far below their point of projection [g=10m/s2]
View Solution
Knowledge Check
Two particles A and B masses 1 kg and 2 kg respectivelty are projected in the same vertical line as shown in figure with speeds uA=200m/s and uB=85m/s respectively. Initially they were 90 m apart. Find the maximum height attained by the centre of mass of the system of particles A and B, from the initial position of centre of mass of the system. Assume that none of these particles collides with the ground in that duration Take g=10m/s2
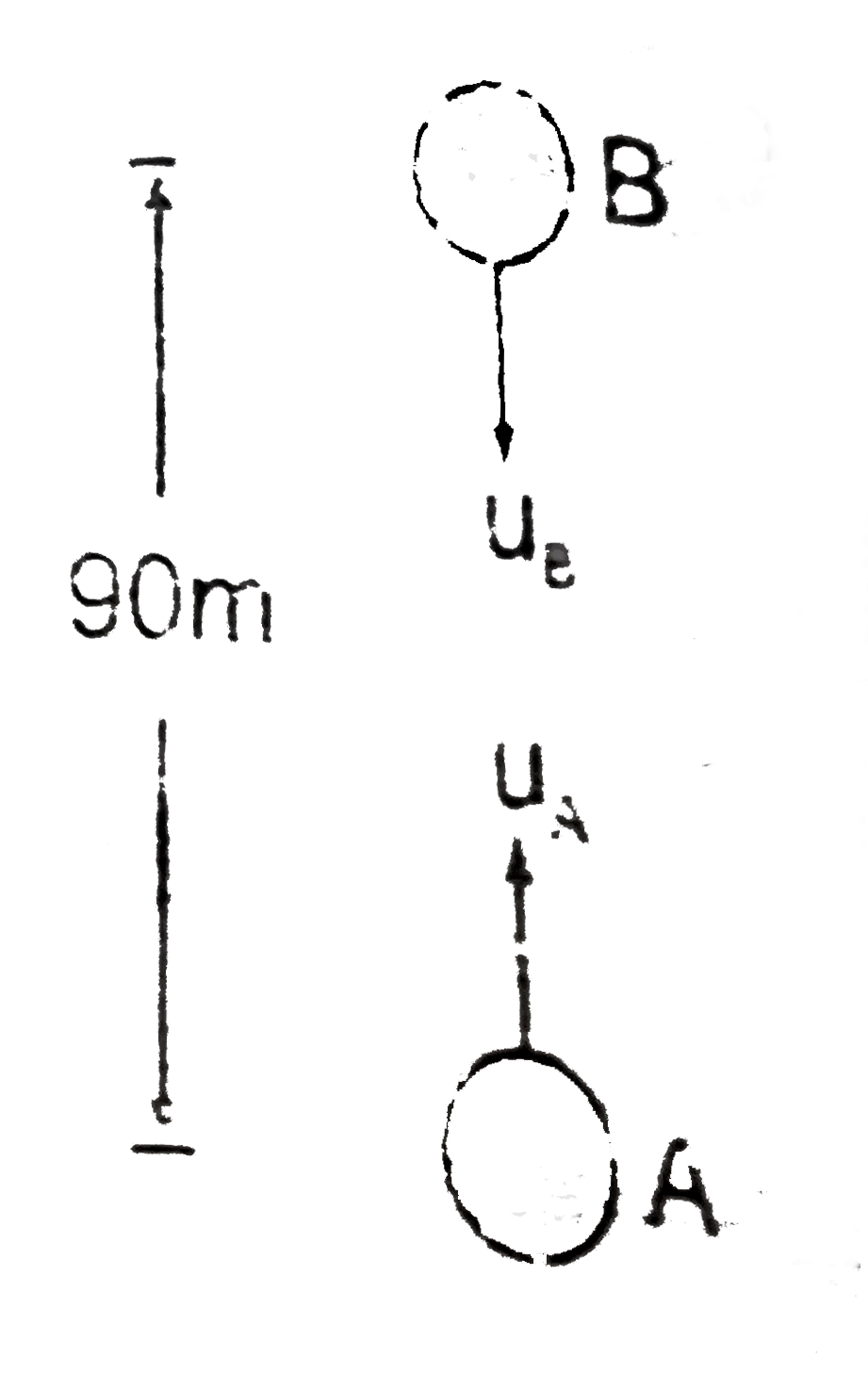 A5 meterB10 meterC25 meterD20 meter
A5 meterB10 meterC25 meterD20 meterTwo particles A and B are projected simultaneously in the direction shown in the figure with velocities VA=20m/s and VB=10m/s respectively. If they collide in air after 1/2 sec. then
 Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3m
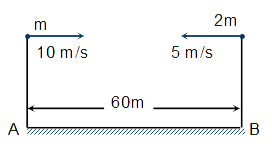
Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3mTwo particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
 A40 mB20 mC30 mDzero
A40 mB20 mC30 mDzero
Two particles A and B are projected simultaneously in the directins shown in figure with velocities vA=20m/sandvB=10m/s respectively. They collide in air after 12 s. Find
(a) the angle θ
(b) the distance x.
 .
.
View SolutionTwo particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then
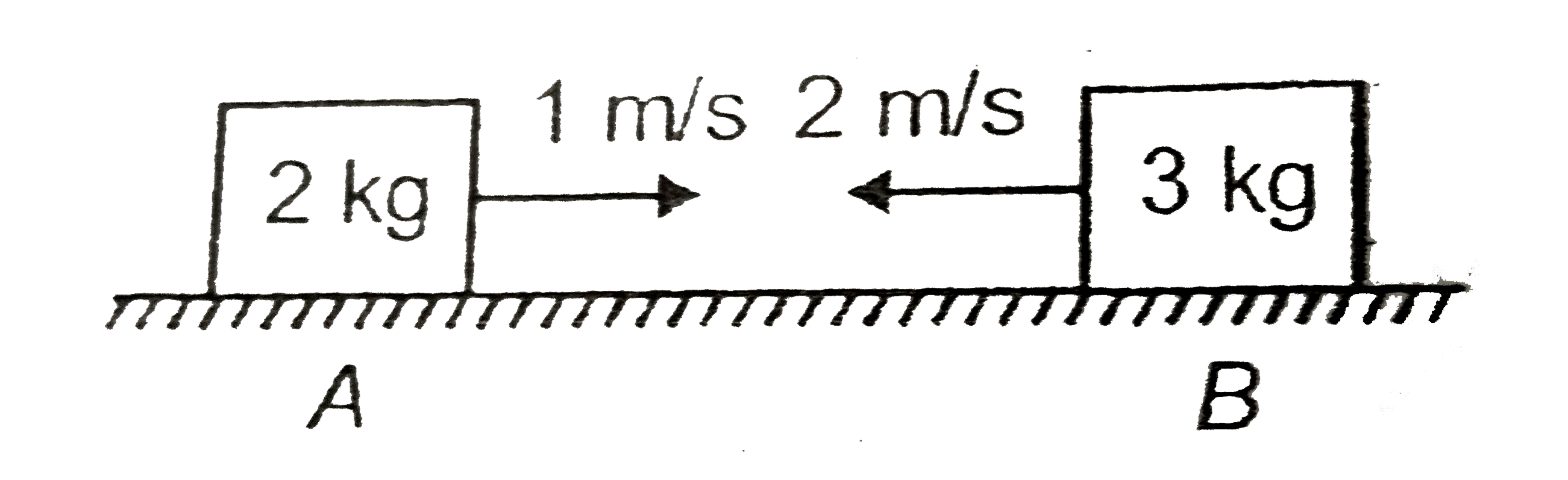
View SolutionTwo particles A and B of equal mass are projected simultaneously with speed 10 m/s each as shown in figure. Find the co-ordinate of COM at t=10 s
View SolutionTwo particles of equal mass are projected simultaneously with speeds 20m/s end 10√3m/s as shown in figure. Find the maximum height reached by the centre of mass of the particles
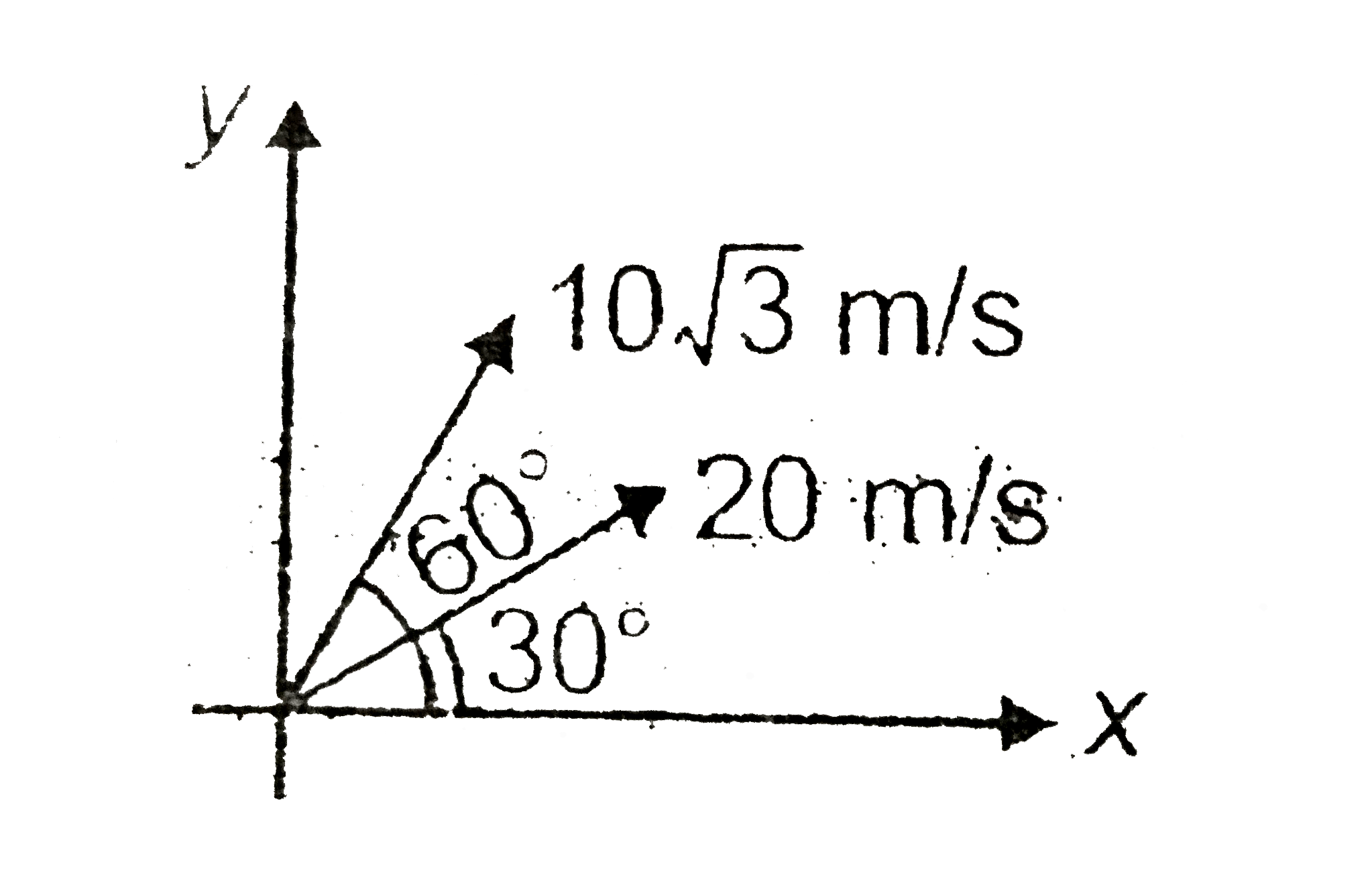
View Solution
