A tube long is closed at one end. A stretched wire is placed near the open end. The wire is long and a mass of . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = .
The correct Answer is:
for the wire,
fundamental frequency
for the closed pipe, frequency of
overtone
since the two frequencies are equal
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Exercise- 3 PART - II
1 Videos
- SOUND WAVESBOOK - RESONANCECHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - IV
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCECHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
A tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .
View SolutionA 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode.A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air =340ms−1.
View Solution
Knowledge Check
A steel piano wire 0.5 m long has a total mass of 0.01 kg and is stretched with a tension of 800 N. The frequency, when it vibrates in its fundamental mode, is
A2 HzB4 HzC100 HzD200 HzA steel wire 0.5 m long has a total mass of 0.02 kg and is stretched with a tension of 800N. The frequency when it vibrates in its fundamental mode is
A2HzB141HzC100HzD200HzIn fundamental mode, the time required for the sound wave to reach upto the closed end of a pipe filled with air is 0.01s. The frequency of vibration of air column is
A2.5HzB15 HzC20 HzD25 Hz
A wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire.

View SolutionConsider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
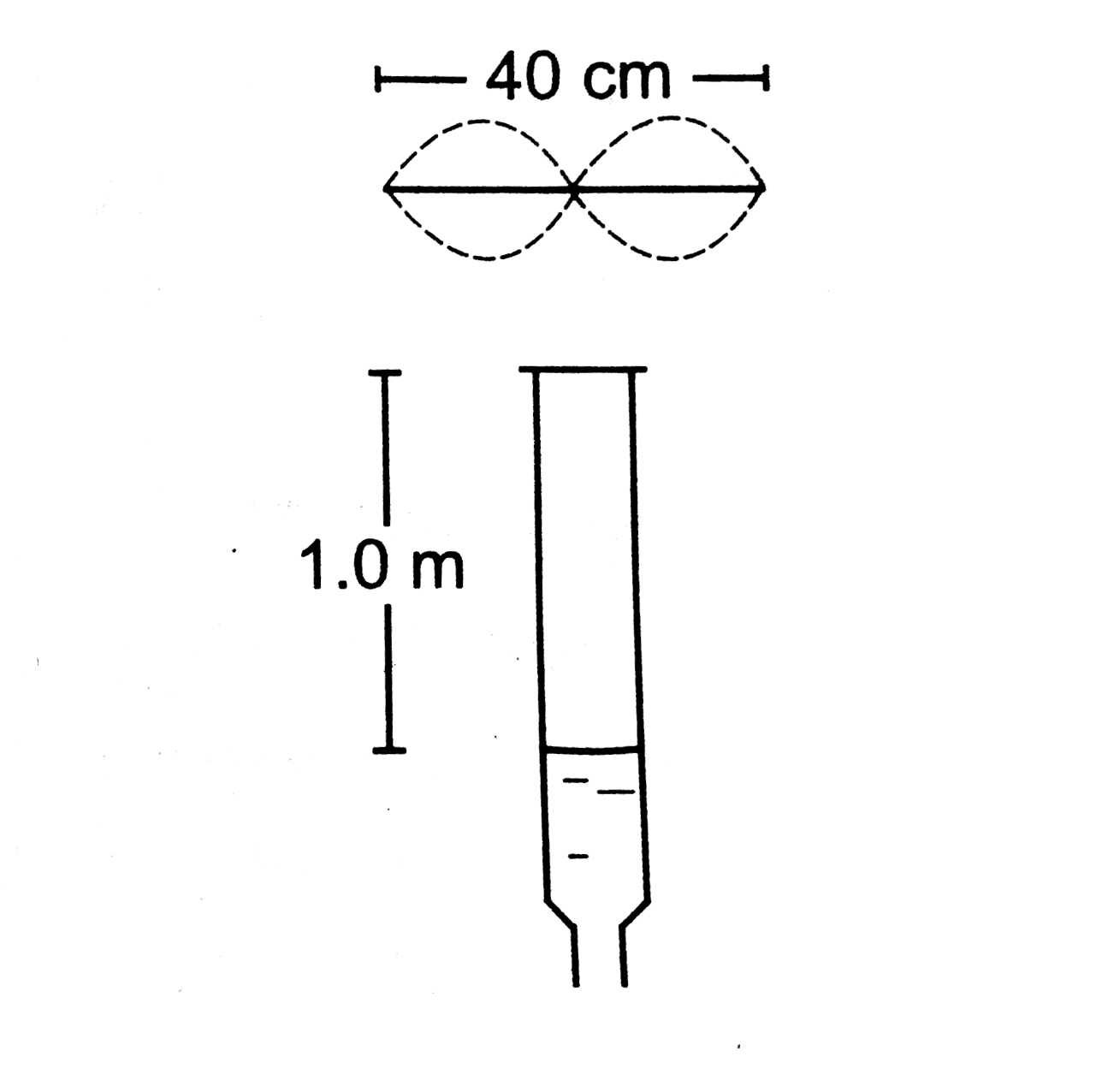 .
.
View SolutionFind the fundamental frequency and the frequency of the third overtone of a pipe 45 cm long. If the pipe is open at both ends (use V=344m/s)
View SolutionA tube 1.0 m long is closed at one end. A wire of length 0.3 m and mass 1×10−2 kg is streched between two fixed ends and is placed near the open end. When the wire is plucked at its mid point the air column resonates in its 1st overtone. Find the tension in the wire if it vibrates in its fundamental mode. [V sound =330m/s].
View SolutionTo decrease the fundamental frequency of a stretched string fixed at both ends one might
View Solution
