Air is initially at 260∘C and 700pa and occupied 0.028m3. The air is expanded at constant pressure to 0.084m3. A polytropic process with n=1.5 is then carried out followed by a constant temperature process which complete the cycle.
(a) sketch cycle in P−V.
(b) find heat received and heat rejected in the cycle.
(c) efficiency of cycle.
P1=700Pa,V2=0.08m3
P1V1=nRT1
No.of moles v=700×0.0288.31×533=0.004mole
T2T1=V2V1=3
T2=3T1=1599K
PVn=C
P(nRTP)n=C
⇒P=C'Tnn−1
P2P3=(1599533)1.5/0.5=33=27.
Q1−2=vCp(T2−T1)=0.004×72×8.31(1599−533)=124J.
Q2−3=ΔU+∫PdV
=vCv(T3−T2)+nR(T2−T3)n−1=vCv(n−γn−1)(T3−T2)
=0.004×52×8.310.10.5(−1066)=−17.7J.
Q31=W31=vRT1ln(V1V3)=0.004×8.31×533ln(P3P1)=−58.4J
(ΣQ)cycle=(Σw)cycle
ΣW=Q1−2+Q2−3+Q3−1=124−17.7−58.4=47.9J.
ηcycle=WnetHeat supplied=47.9106×100=38.6%

Topper's Solved these Questions
Similar Questions
The density (ρ) versus pressure (p) graph of one mole of an ideal monoatomic gas undergoing a cyclic process is shown in figure. Molecular mass of gas is M.
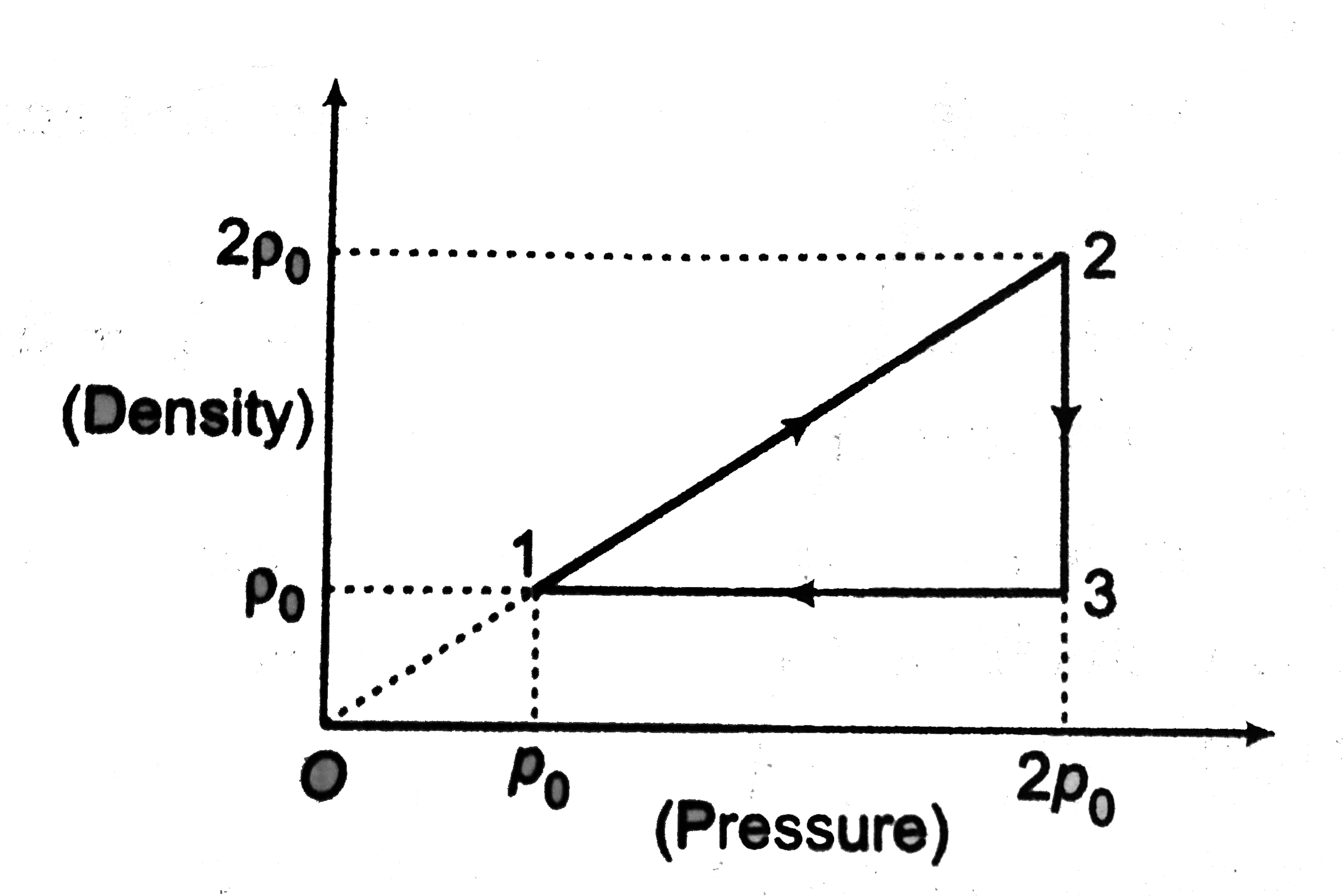
(a) Find work done in each process.
(b) Find heat rejected by gas in one complete cycle.
(c) Find the efficiency of the cycle.
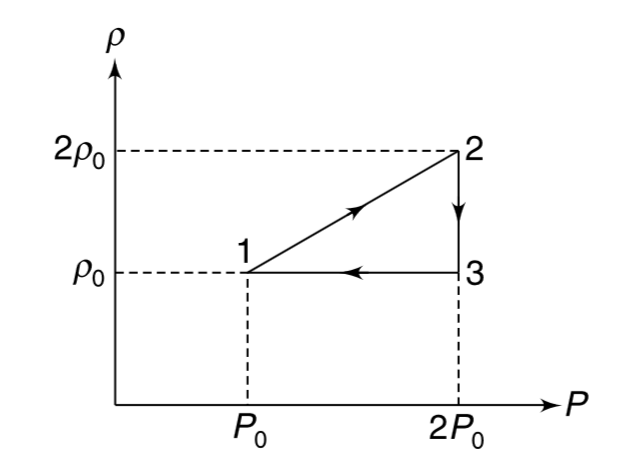
View SolutionOne mole of a mono atomic gas of molar mass M undergoes a cyclic process as shown in the figure. Here ρ is density and P is pressure of the gas.
(a) Calculate the heat rejected by the gas in one complete cycle.
(b) Find the efficiency of the cycle.
View SolutionAir that initially occupies 0.280 m at a gauge pressure of 103.0 kPa is expanded isothermally to a pressure of 101.3 kPa and then cooled at constant pressure until it reaches its initial volume. It then returns to its initial pressure in a constant-volume process. Compute the network done by the air. (Gauge pressure is the difference between the actual pressure and atmospheric pressure.)
View SolutionAn ideal monoatomic gas occupies volume 10−3m3 at temperature 3K and pressure 103Pa. The internal energy of the gas is taken to be zero at this point. It undergoes the following cycle: The temperature is raised to 300K at constant volume, the gas is then expanded adiabatically till the temperature is 3K , followed by isothermal compression to the original volume . Plot the process on a PV diagram. Calculate (i) The work done and the heat transferred in each process and the internal energy at the end of each process, (ii) The thermal efficiency of the cycle.
View SolutionIn a heat engine, the temperature of the source and sink are 500 K and 375 K. If the engine consumes 25×105J per cycle, find(a) the efficiency of the engine, (b) work done per cycle, and (c) heat rejected to the sink per cycle.
View SolutionAn ideal gas with a known γ, completes a cycle consisting of two isotherms and two isobars. The isothermal processes are executed at temperatures T and T'(<T) and isobaric processes are completed at pressures P0 and eP0 [e = base of natural logarithm]. Find the efficiency of the cycle.
View Solution10 gm of oxygen at a pressure 3×105N/m2 and temperature 10∘C is heated at constant pressure and after heating it occupies a volume of 10 litres. (a) Find the amount of heat received by the gas and (b) the energy of thermal motion of gas molecules before heating.
View SolutionOne mole of a gas is carried through the cycle shown in Fig. The gas expands at constant temperature T from volume V to 2V. It is them compressed to the initial volume at constant pressure and is finally brought back to its original state by heating at constant volume. Calculate the work done by the gas in complete cycle.

View SolutionA reversible heat engine carries 1 mole of an ideal monatomic gas aroung the cycle 1-2-3-1. Process 1-2 takes place at constant volume, process 2-3 take place at constant volume, process 2-3 is adiabatic, and process 3-1 takes place at constant pressure. Complete the values for the heat ΔQ, the change in internal energy ΔU, and the work done Δ, for each of the three processes and for the cycle as a whole.

View SolutionThree moles of an ideal gas (Cp=72R) at pressure, PA and temperature TA is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally gas is compressed at constant volume to its original pressure PA.
(a) Sketch P-V and P-T diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
View Solution
