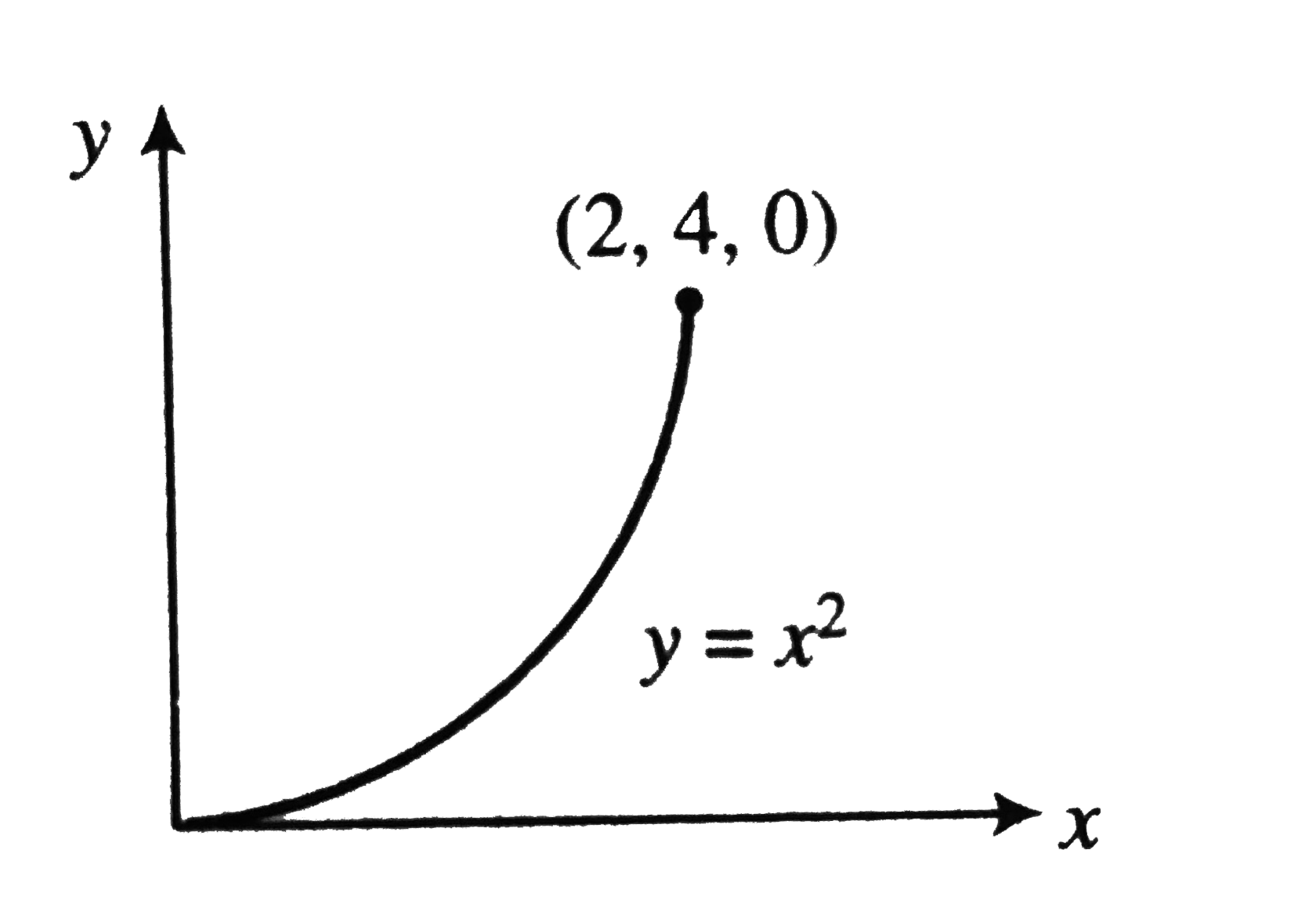
A force $\to F = (3 x y - 5 z) ˆ j + 4 z ˆ k$ is applied on a particle. The work done by the force when the particle moves from point $(0, 0, 0)$ to point $(2, 4, 0)$ as shown in figure.

$\frac{280}{5}$

$\frac{140}{5}$

$\frac{232}{5}$

$\frac{192}{5}$

Video Solution

Text Solution

Verified by Experts

The $z$ -component of the force and the $x$ -component of displacement are ieffective here.
$d W = F_{y} d y = 3 x y . d y$ ( $∵ z = 0$ )
$= 6 x^{4} d x$ ( $∵ y = x^{2}$ )
Integrating between $x = 0$ and $x = 2$ gives the result.

Updated on:21/07/2023

A force of $\to F = 2 x ˆ i + 2 ˆ j + 3 z^{2} ˆ k N$ is acting on a particle. Find the work done by this force in displacing the body from $(1, 2, 3) m$ to $(3, 6, 1) m$ .
A(a) $- 10 J$
B(b) $100 J$
C(c) $10 J$
D(d) $1 J$
A force of $F = (0.5 x + 12) N$ acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
A128 J
B80 J
C64 J
D52 J
A force $¯ ¯ ¯ F =$ (3 hati-4 hatj +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
A-3
B-2
C2
D3