A particle of mass m is going along surface of smooth hemisphere of radius R in verticle plane. At the moment shown its speed is v. Choose correct option(s).

A

$m g - N cos θ = m (g {sin}^{2} θ - \frac{v^{2}}{R} cos θ)$

B

$N - m g cos θ = \frac{m v^{2}}{R}$

C

$m g - N sin θ = \frac{m v^{2}}{R}$

D

$N sin θ = m (g sin θ cos θ - \frac{v^{2}}{R} sin θ)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

$m g - N cos θ = m g sin θ - m \frac{v^{2}}{R} cos θ$
$N sin θ = \frac{m v^{2}}{R} sin θ + m g cos θ sin θ$
$N - m g cos θ = \frac{m v^{2}}{R}$

|

Updated on:21/07/2023

Class 12 PHYSICS MASTER PRACTICE PROBLEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass $m$ initially at rest starts moving from point $A$ on the surface of a fixed smooth hemisphere of radius $r$ as shown. The particle looses its contact with hemisphere at point $B . C$ is centre of the hemisphere. The equation relating $θ$ and $θ'$ is
.
A $3 sin θ = 2 cos θ'$
B $2 sin θ = 3 cos θ'$
C $3 sin θ' = 2 cos θ$
D $2 sin θ = 3 cos θ'$
Question 2 - Select One
The sphere $A$ of mass $m_{1}$ moves with velocity $V$ on a frictionless horizontal surface and strikes with sphere $B$ of mass $m_{2}$ at rest. The sphere $A$ comes back with speed $V / 10$ . Choose the correct option.

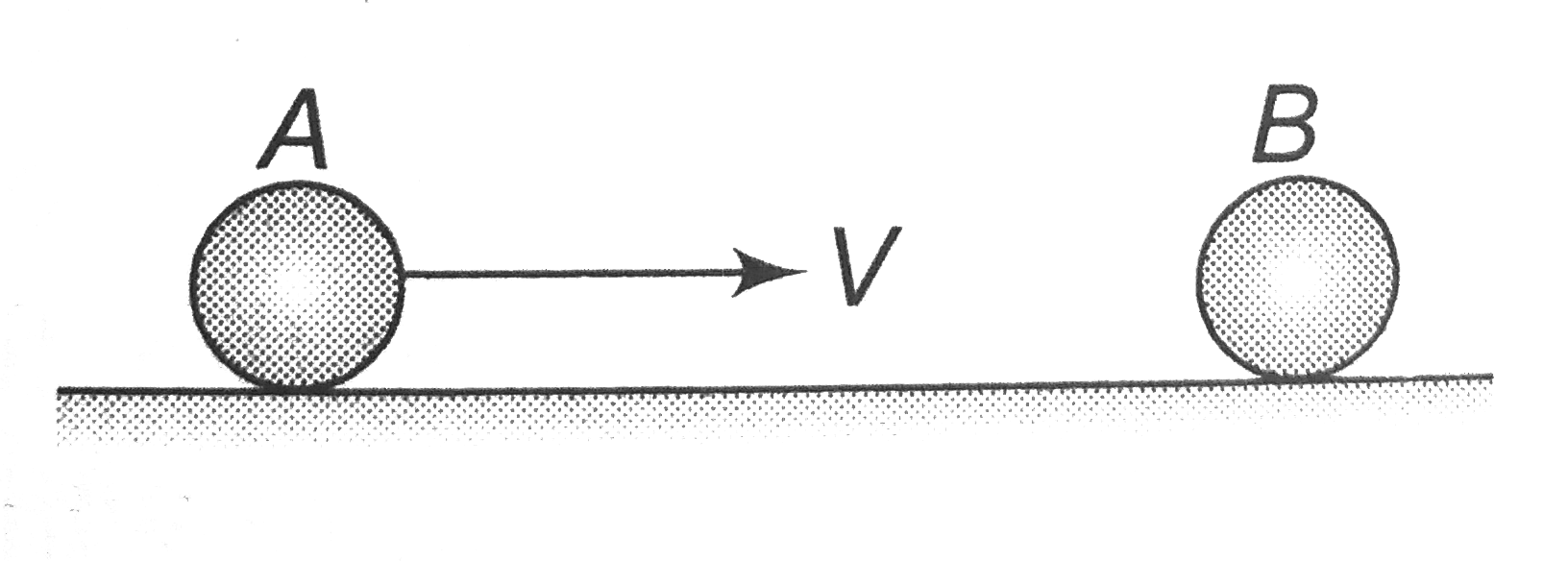A $m_{1} > m_{2}$
B $m_{1} = m_{2}$
C $m_{1} < m_{2}$
Dnone of these
Question 3 - Select One
A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
A $m g = \frac{m v^{2}}{r}$
B $m g > \frac{m v^{2}}{r}$
C $m g \leq \frac{m v^{2}}{r}$
D $m g \geq \frac{m v^{2}}{r}$

BANSAL-MASTER PRACTICE PROBLEM-Multiple objective

Home
Ask Doubt
Profile