A beam of electrons has radius r and contains 'n' electrons per cubic meter moving with velocity →v along the beam (figure). Assume that a beam that is much longer than its diameter forms a cylinderically symmetric distribution of charge and current. The beam expands if the electric force exceeds the magnetic force. So long as the expansion is slow, the approximations of cylindrical symmetry and static fields remain valid.
A beam of electrons has radius r and contains 'n' electrons per cubic meter moving with velocity vec(v) along the beam (figure). Assume that a beam that is much longer than its diameter forms a cylinderically symmetric distribution of charge and current. The beam expands if the electric force exceeds the magnetic force. So long as the expansion is slow, the approximations of cylindrical symmetry and static fields remain valid. What is electric field produced on the edge of the beam? What is electric field produced on the edge of the beam?

A

→E=ner4ɛ0ˆr

B

→E=ner2ɛ0ˆr

C

→E=−ner4ɛ0ˆr

D

→E=−ner2ɛ0ˆr

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

The total charge inside the cylinder is Q=−neπr2l
Applying Gauss's law givesϕE=Q/∈0
2πrlEr=−neπr2l∈0⇒→E=−ner2∈0ˆr
The circulation of →B around the circle is ɛ=2πrB0
The position direction for current is along the axis parallel to →v
The current passing through the circle is
I=−πr2j=−πr2≠v
Applying Ampere's law we obtain ɛ=μ0I
2πrB0=−μ0πr2≠v⇒→B=12μ0≠vr(−ˆθ)
The total force acting on an electron is the sum of the electric and magnetic forces
→F=−e(→E+→v×→B)=e(ner2∈0−μ0nerv22)ˆr=ne2r2∈0(1−μ0∈0v2)ˆr]
ocr_image

Updated on:21/07/2023
|
Class 12PHYSICSMASTER PRACTICE PROBLEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A beam of electrons has radius r and contains 'n' electrons per cubic meter moving with velocity →v along the beam (figure). Assume that a beam that is much longer than its diameter forms a cylinderically symmetric distribution of charge and current. The beam expands if the electric force exceeds the magnetic force. So long as the expansion is slow, the approximations of cylindrical symmetry and static fields remain valid.
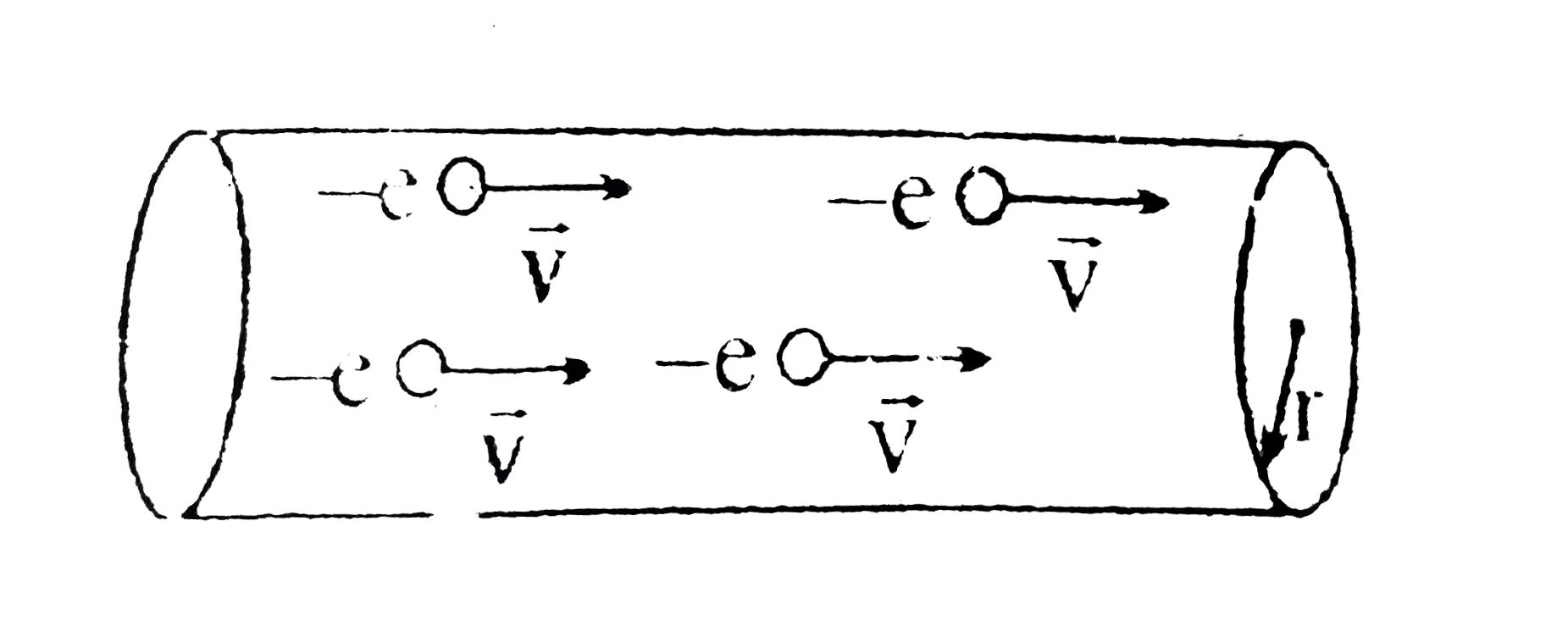
    ocr_image
    What is net force on the electron at the edge of the beam?

    A(2n e^(2)r)/(varepsilon_(0)) (1-mu_(0)varepsilon_(0)v^(2))hat(r)
    Bne2r2ɛ0(1−μ0ɛ0v2)ˆr
    C4ne2rɛ0(1−μ0ɛ0v2)ˆr
    Dne2r4ɛ0(1−μ0ɛ0v2)ˆr

  • A beam of electrons starts to accelerate from rest due to a uniform electric field in vacuum, the moving electrons:

    Ainitially experience a force of mtual repulsion
    Bexperience a force of mutual attraction after travelling a certain distance
    Cwill continue to diverge due to electrostatic repulsion
    Dwill follow parallel lines because there is no force of attraction between them.

  • Two streams of electrons are moving parallel to each other in the same direction. They

    Aa net repulsion between them
    Ba net attraction between them
    Cthe electric repulsion and magnetic attraction nullify each other
    Dthe electric repulsion and magnetic repulsion nullify each other