All bodies, no matter how hot or cold, continuously radiate photons. At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum. Figure illustrates how the intensity per unit wavelength depends on wavelength for a perfect blackbody emitter. Although this figure can strictly be applied only to a black body, yet this will approximately discribe the behavior of many of the self radiating systems. For example, sun has an approximate temperature of 6000K. it is not a black body, it has an emissivity of nearly $0.6$ But its peak almost occurs at a wave length that predicted by Wein's law. Suppose we have a bulb of power 100W. It emits only about 5W as visible light, rest is emitted as infrared radiated. Assume that the bulb filament has a surface area of 10mm^(2) $(h c = 1250 e V - n m)$

Assume that the light emitted by the bulb in the visible region is entirely of wavelength 500 nm. What is the number of photons emitted per second in the visible region?

$1.25 \times 10^{19}$

$5 \times 10^{19}$

$2.5 \times 10^{19}$

$4 \times 10^{19}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$5 W = \frac{d N}{d t} \times \frac{h c}{λ} = \frac{d N}{d t} \times \frac{1240}{500} \times 1.6 \times 10^{- 19}$
$\frac{d N}{d t} = \frac{2500 \times 10^{19}}{1240 \times 1.6} = 1.25 \times 10^{19}$

Updated on:21/07/2023

Class 12 PHYSICS MASTER PRACTICE PROBLEM

Topper's Solved these Questions

Knowledge Check

All bodies, no matter how hot or cold, continuously radiate photons. At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum. Figure illustrates how the intensity per unit wavelength depends on wavelength for a perfect blackbody emitter. Although this figure can strictly be applied only to a black body, yet this will approximately discribe the behavior of many of the self radiating systems. For example, sun has an approximate temperature of 6000K. it is not a black body, it has an emissivity of nearly $0.6$ But its peak almost occurs at a wave length that predicted by Wein's law. Suppose we have a bulb of power 100W. It emits only about 5W as visible light, rest is emitted as infrared radiated. Assume that the bulb filament has a surface area of 10mm^(2) $(h c = 1250 e V - n m)$

What is the approximate temperature of the filament?
A500 k
B350 k
C2500 K
D10000 K
All bodies, no matter how hot or cold, continuously radiate photons. At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum. Figure illustrates how the intensity per unit wavelength depends on wavelength for a perfect blackbody emitter. Although this figure can strictly be applied only to a black body, yet this will approximately discribe the behavior of many of the self radiating systems. For example, sun has an approximate temperature of 6000K. it is not a black body, it has an emissivity of nearly $0.6$ But its peak almost occurs at a wave length that predicted by Wein's law. Suppose we have a bulb of power 100W. It emits only about 5W as visible light, rest is emitted as infrared radiated. Assume that the bulb filament has a surface area of 10mm^(2) $(h c = 1250 e V - n m)$

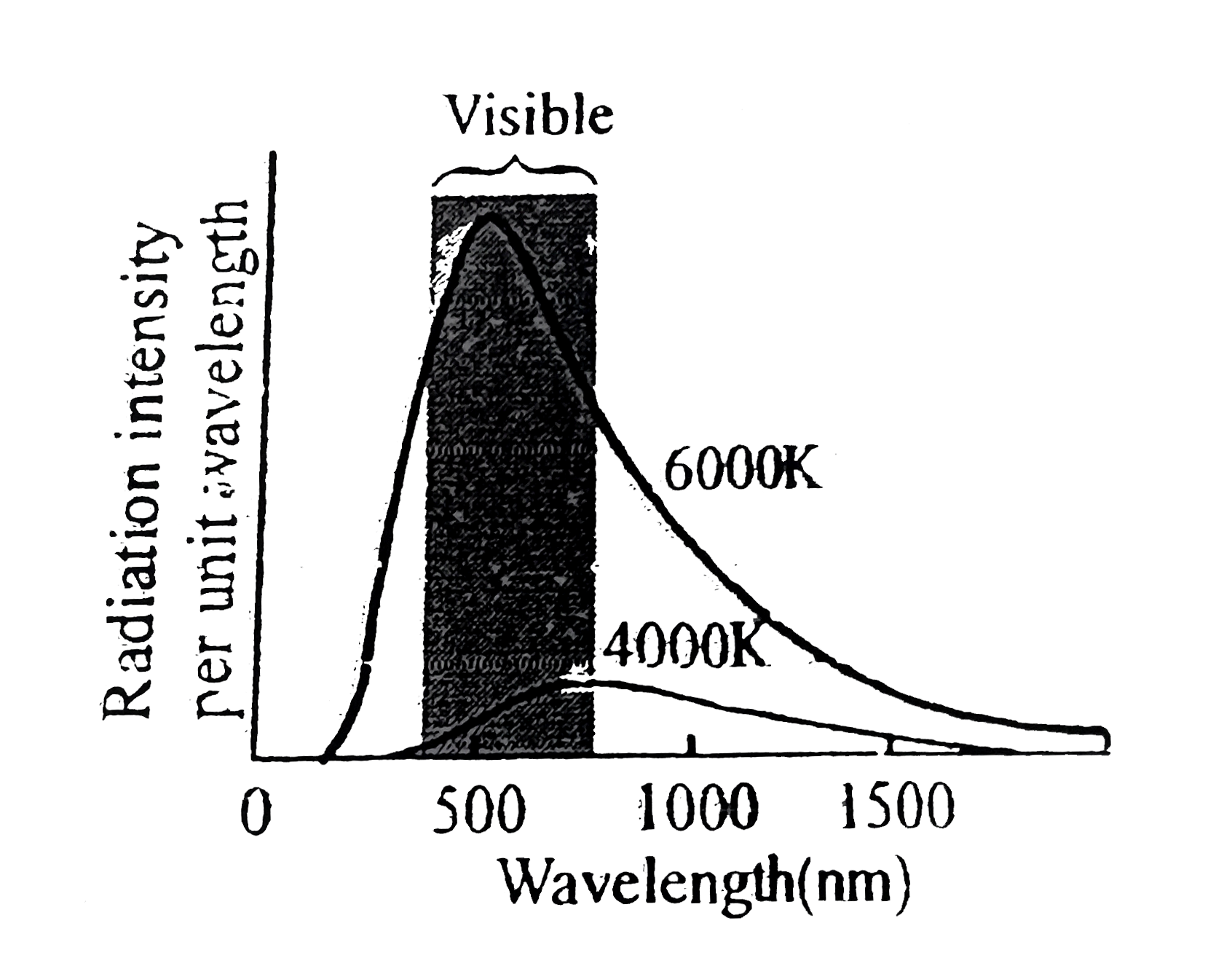
If we want of increase the number of photons emitted by the bulb in the visible region without changing the wattage, which method would be most appropriate?
Aincreasing emissivity by a factor of 2
Bincreasing the radius of the filament by a factor of 2 and the length by a factor of 4.
Cdecreasing the radius of the filament by a factor of 2 and the length by a factor of 4
Ddoubling the voltage and decreasing the length of the filament by a factor of 2.
All bodies, no matter how hot or cold, continuously radiate photons. At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum. Figure illustrates how the intensity per unit wavelength depends on wavelength for a perfect blackbody emitter. Although this figure can strictly be applied only to a black body, yet this will approximately discribe the behavior of many of the self radiating systems. For example, sun has an approximate temperature of 6000K. it is not a black body, it has an emissivity of nearly $0.6$ But its peak almost occurs at a wave length that predicted by Wein's law. Suppose we have a bulb of power 100W. It emits only about 5W as visible light, rest is emitted as infrared radiated. Assume that the bulb filament has a surface area of 10mm^(2) $(h c = 1250 e V - n m)$

Which of the following resistances would have maximum surface temperature. All of them have a surface area of $10 m m^{2}$ and same emissivity

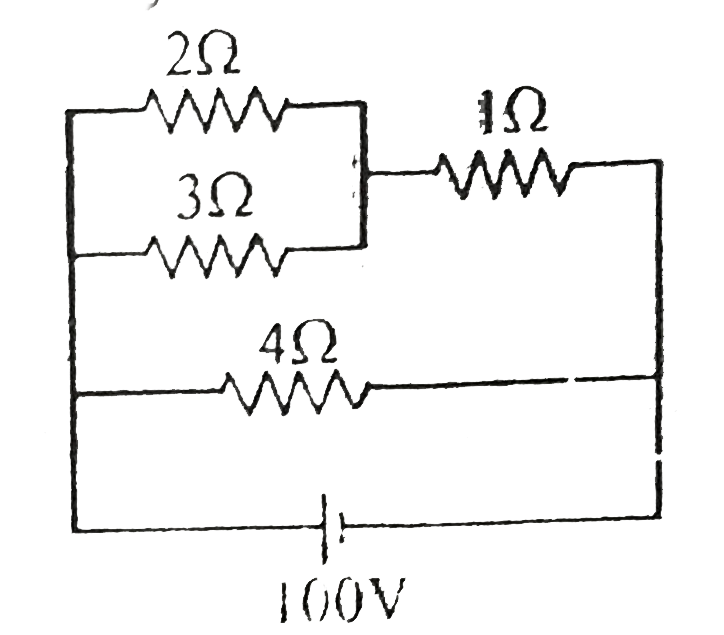A $1 Ω$
B $2 Ω$
C $3 Ω$
D $4 Ω$