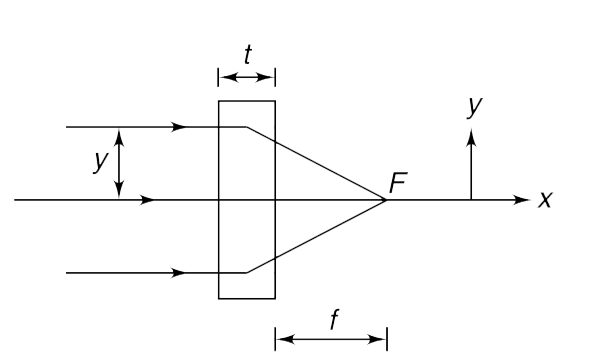
A parallel beam of light travelling in x direction is incident on a glass slab of thickness t. The refractive index of the slab changes with y as μ=μ0(1–y2y02)where μ0 is the refractive index along x axis and y0 is a constant. The light beam gets focused at a point F on the x axis. By using the concept of optical path length calculate the focal length f. Assumef>>t and consider y to be small.
Z20/(2μ0t)
Z20/(μ0t)
μ0Z20/(2t)
None
The correct Answer is:A
On comparing optical path we get
tμ0(1−Z2Z0)+√Z2+F2=tμ0+F
⇒√Z2+F2=μ0tZ2Z20+F
⇒Z2+F2=μ20t2(Z2Z20)2+F2+2μ0tZ2Z20F
since is very small
⇒Z2=2μ0tZ2Z20F⇒F=Z20/(2μ0t)
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
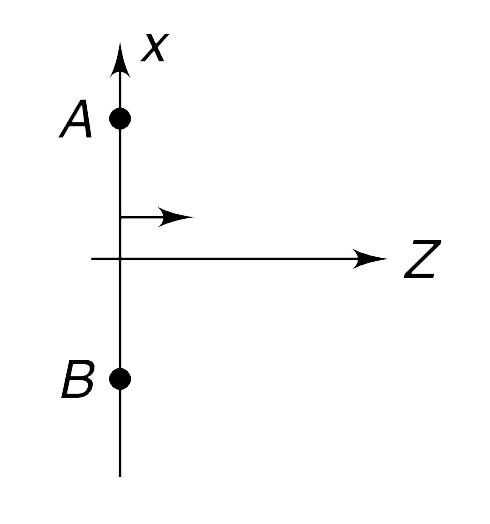
The refractive index of a medium changes asμ=μ0[1−x2+y2d2]1/2where μ0 is the refractive index on the z axis. A plane wavefront (AB) is incident along z axis as shown in the figure. Draw the wavefront at a later timeΔt. Is the wavefront getting focused?
View SolutionA ray of light is incident at an angle of 60∘ on one face of a rectangular glass slab of thickness 0.1m, and refractive index 1.5.Calculate the lateral shift produced.
View Solution
Knowledge Check
A monochromatic light of wavelength 4800 A travelling in air is incident on a glass slab of refractive index 1.5, its wavelenght in glass slab is
A5000 ÅB4800 ÅC3500 ÅD3200 ÅThe time taken by a ray of light to travel through a glass slab of thickness 2 cm and refractive index 1.5 will be
A10^(-8) sB10−10sC2×10−8sD10−12sA parallel beam of monochromatic light is incident on a glass slab at an angle of 35∘. The ratio of width of beam in glass to that in air is [ μg=1.5]
A1.07B1.13C3.21D4.28
A ray of light of wavelength u0 and frequency v0 enters a glass slab of refractice index μ from air. Then
View SolutionA ray of light is incident on a glass slab at an angle of 45∘. If refractive index of glass be 1.6, what is the angle of refraction ?
View SolutionA ray of light passes throught a plane glass slab of thickness t and refractive index μ=1.5. The angle between incident ray and emergent ray will be
View SolutionA ray of light is incident on a glass slab of thickness t, at an angle i,r is the angle of refraction in the glass slab. Distance travelled in the glass slab is
View SolutionA beam of light travelling at a velocity of v m/s is incident at
an angle 45∘ on a glass slab of refractive index 1.5. What is
the velocity of the beam of light inside the slab ?
View Solution
