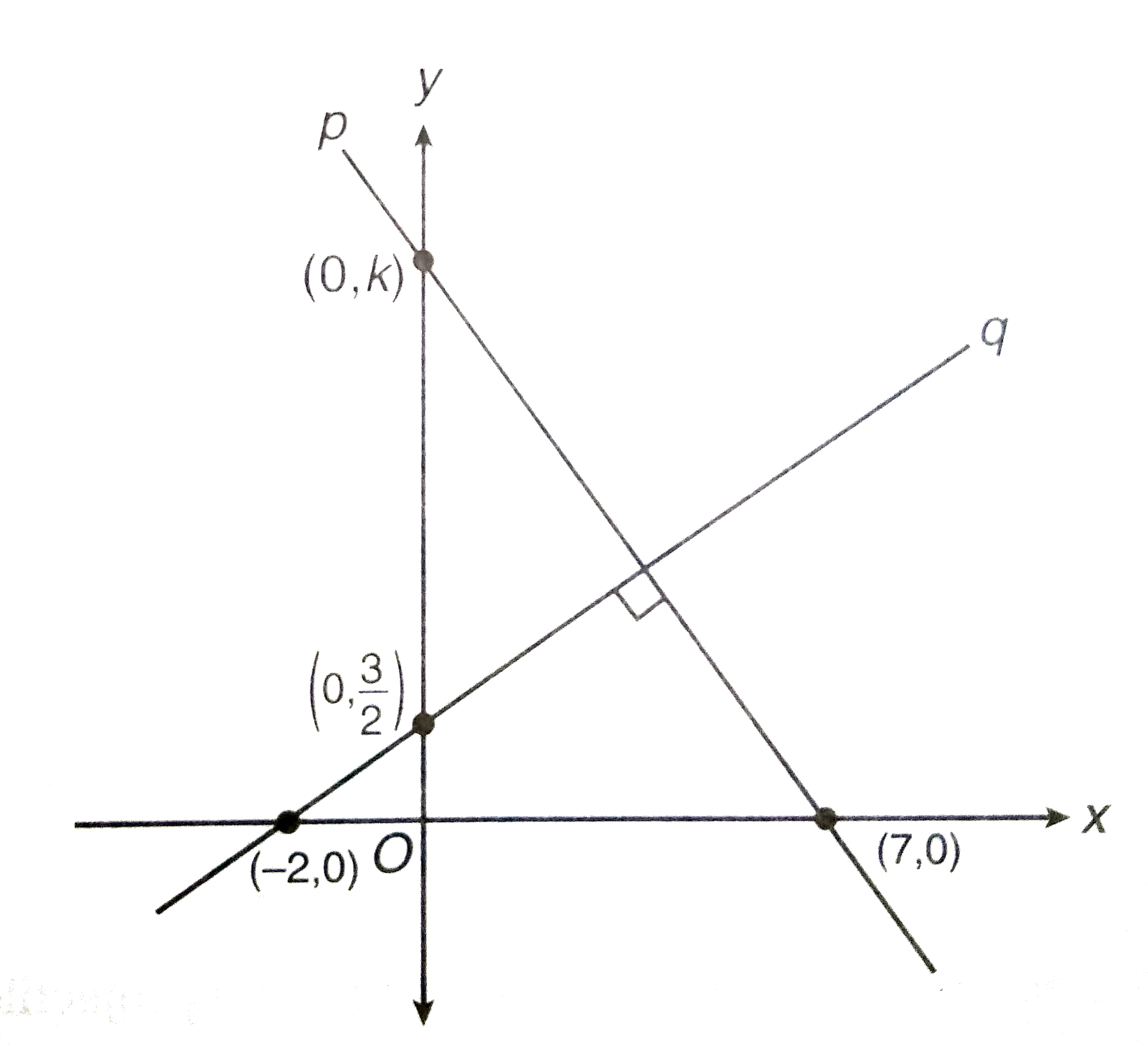
Line p contains the points . If line p is parallel to line q whose equation of . What is the value of k?
The correct Answer is:
To find the value of k such that line p is parallel to line q, we will follow these steps:
Step 1: Find the slope of line p
Line p passes through the points (−1,8) and (9,k). The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
m=y2−y1x2−x1
Here, (x1,y1)=(−1,8) and (x2,y2)=(9,k). Therefore, the slope mp of line p is:
mp=k−89−(−1)=k−810
Step 2: Find the slope of line q
The equation of line q is given as 3x+4y=7. We need to convert this into slope-intercept form y=mx+c.
Rearranging the equation:
4y=−3x+7
y=−34x+74
From this, we can see that the slope mq of line q is:
mq=−34
Step 3: Set the slopes equal to each other
Since lines p and q are parallel, their slopes must be equal:
mp=mq
Substituting the slopes we found:
k−810=−34
Step 4: Solve for k
To solve for k, we cross-multiply:
4(k−8)=−30
Expanding this gives:
4k−32=−30
Adding 32 to both sides:
4k=2
Dividing both sides by 4:
k=24=12
Final Answer
Thus, the value of k is:
12
Line p passes through the points (−1,8) and (9,k). The formula for the slope m between two points (x1,y1) and (x2,y2) is given by:
The equation of line q is given as 3x+4y=7. We need to convert this into slope-intercept form y=mx+c.
y=−34x+74
Since lines p and q are parallel, their slopes must be equal:
To solve for k, we cross-multiply:
Thus, the value of k is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
The slope of the line parallel to the line whose equation is 2x+3y=8 is
A−2B−32C−23D23If the line y+2x+3=0 is parallel to the line 2y-px-4=0 , what is the value of p ?
A−4B−2C2D4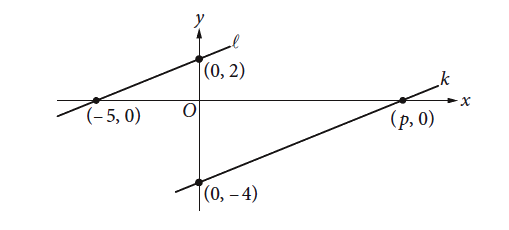
In the xy-plane above, line l is parallel to line k. What is the value of p ?A4B5C8D10
Point P divides the line segment joining the points A(−1, 3) and B(9, 8) such that APBP=k1 . If P lies on the line x−y+2=0 , find the value of k .
View SolutionPoint P divides the line segment joining the points A(2,1) and B(5,−8) such that APAB=13. If P lies on the line 2x−y+k=0, find the value of k.
View SolutionPoint P divides the line segment joining the points A(2,1) and B(5,−8) such that APAB=13. If P lies on the line 2x−y+k=0, find the value of k.
View SolutionThe line joining the points (2, 1) and (5, −8) is trisected at the points P and Q . If point P lies on the line 2x−y+k=0 . Find the value of k .
View SolutionPoint P divides the line segment joining the points A(2,1)andB(5,−8) such that APAB=13. If P lies on the line 2x - y + k =0, find the value of k.
View Solution