The mean of 24 test scores is 77.5. When the 25th class member takes the test, the mean down by 1.1 points. What was that 25h score?
To solve the problem step-by-step, we can follow these calculations:
Step 1: Calculate the sum of the first 24 test scores.
Given that the mean of the 24 test scores is 77.5, we can use the formula for the mean:
Mean=Sum of scoresNumber of scores
Rearranging this gives us:
Sum of scores=Mean×Number of scores
Substituting the known values:
Sum of scores=77.5×24
Calculating this:
Sum of scores=1860
Step 2: Determine the new mean after the 25th score is added.
According to the problem, the mean decreases by 1.1 points when the 25th student takes the test. Therefore, the new mean is:
New Mean=77.5−1.1=76.4
Step 3: Set up the equation for the new sum of scores.
The new sum of scores after adding the 25th score can be expressed as:
New Sum of scores=Old Sum of scores+25th score
So we can write:
New Mean=New Sum of scoresNumber of scores
Substituting the known values:
76.4=1860+25th score25
Step 4: Solve for the 25th score.
To eliminate the fraction, we multiply both sides by 25:
76.4×25=1860+25th score
Calculating the left side:
1910=1860+25th score
Now, we can isolate the 25th score:
25th score=1910−1860
Calculating this gives:
25th score=50
Conclusion:
The score of the 25th student is 50.
---
Given that the mean of the 24 test scores is 77.5, we can use the formula for the mean:
According to the problem, the mean decreases by 1.1 points when the 25th student takes the test. Therefore, the new mean is:
The new sum of scores after adding the 25th score can be expressed as:
To eliminate the fraction, we multiply both sides by 25:
The score of the 25th student is 50.
Topper's Solved these Questions
- STATISTICSBOOK - ENGLISH SATCHAPTER - STATISTICSEXERCISE - EXERCISES
8 Videos
- SOLVING POLYNOMIAL INEQUALITIES BOOK - ENGLISH SATCHAPTER - SOLVING POLYNOMIAL INEQUALITIES EXERCISE - EXERCISES
3 Videos
- STRATEGIES FOR SOLVING SAT MATH PROBLEMS BOOK - ENGLISH SATCHAPTER - STRATEGIES FOR SOLVING SAT MATH PROBLEMS EXERCISE - EXAMPLE
19 Videos
Similar Questions
The mean score of 8 players in a basketball game was 14.5 points. IF the highest individual score is removed, the mean score of the remaining 7 players becomes 12 points. What was the highest score?
View SolutionIf the median of the scores 1,2,x,4,5(where 1<2<x<4<5) is 3, then the mean of the scores is
View Solution
Knowledge Check
A student's mean score on 5 tests was 84. The student's mean score on the first 4 of these tests was 87. What was the student's score on the fifth of these tests ?
A68B72C75D81the arithmetic mean of a set of 20 test scores is represented by x. If each scores is increased by y points, which expression represents the arithmetic mean of the revised set of test scores?
Ax+yBx+20yCx+y20Dx+y20The average of the test scores of a group of x students is 76 and the average of the test scores of a group of y students is 90. When the scores of the two groups of students are combined, the average test score is 85. What is the value of of xy?
A47B59C23D74
Calculate the mean of the scores of 20 students in a mathematics test
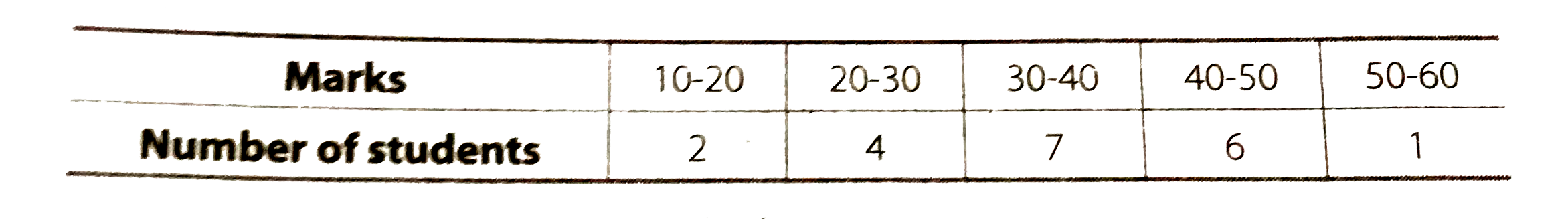
View Solution
The frequency chart shows test scores for a certain class. The total number of student is 31. If a student in the class was picked at random , what is the probability that the student's score was below 71 ?
View SolutionOn a test that has a normal distribution of scores of 59 falls two standard deviations below the mean, and score of 74 is one standard deviation above the mean. If x is an integer score that lies between 2.5 and 3.0 standard deviations above the means. What is a possible value of x?
View SolutionA student scores the following marks in five tests 45, 54, 41, 57, 43. His score is not known for the sixth test. If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is
View SolutionIn a particular college, the test scores of the most recent test given for a particular Physics class and a particular Literature class were studied. Both tests were scored from 0 to 100 and had a total of 20 question, which were equally weighted with no partial credit. The physics class had 128 students and the Literature class had 75 students . The test results are shown in the two graphs below.

The dean of the college is comparing the scores from the two classes and calculates the median for each class. If the dean labels the median score of the Physics class P and the median score of the Literature class L, what is the sum of P and L?
View Solution
