Question

Probability

Explanation

How to find Probability?

In this lesson, we will discuss the concept of probability. We will also concentrate on the probability formula along with some examples to make things easier to understand. The term ‘probability’ means ‘possibility.’

Probability is that branch of mathematics that deals with the occurrence of a random event. The expression of value is between zero and one. In Maths, probability has been introduced for predicting how likely the events are to happen. In the probability distribution, this is the basic probability theory that is used. It is important to know the possible number of outcomes in order to find the probability of a single event to occur.

What is probability in Math?

The measure of the likelihood of an event to occur is known as probability. You should understand that you can never predict many events with total certainty. It is possible to predict only the chance of an event that is supposed to occur.

In other words, we can predict how likely they are to happen by using it. In probability, the range can be between 0 to 1. Here, you should understand that 0 is the event that is going to be an impossible one, while 1 indicates a certain event. For students of Class 10, the probability is an important topic where it is important to get the right understanding about it in the best way.

We can take an example of tossing a coin up in the air. Here, you can always expect two probable outcomes which are either Head or Tail (H, T). On the other hand, we toss two coins in the air, then there will be an occurrence of three possible outcomes. One of the coins would show head or even both show heads or tails while in another instance, it might show heads and one tail such as (H,H), (H, T), (T, T).

What is Probability Formula?

When the possibility of an event to happen is the same as the ratio of the total number of outcomes or favourable outcomes, then this is known as the probability formula.

Probability of event to happen P(E) = Number of favourable outcomes/Total Number of outcomes

There are times when students mistook “desirable outcome” with “favourable outcome.” But students should be clear that for different situations or events, they can find more formulas for it.

We will elucidate it with some solved examples.

Question 1:  There are 6 gems in a table. Out of them 3 are red, 1 is blue, and 2 are yellow. Can you tell the probability of picking a yellow gem?

Answer: Here, the probability is equal to the number of yellow gems in the table, divided by the total number of gems. So, here, 2/6 = 1/3

Question 2:   A coin is tossed 1000 times with the following frequencies:

Head: 450, Tail: 550

When a coin randomly tossed, what is the probability to get:

(i) A head?

(ii) A tail?

Solution:

The total number of times a coin is tossed = 1000

Number of times of heads = 450

Number of times of tails = 550

(i) Probability of getting head = the number of heads/total number of trails

= (450/1000)

= 0.450

(ii) Probability of getting tail = the number of tail/total number of trails

= (550/1000)

= 0.550

Related Videos:

• Primary data


• Secondary data


• Presentation of data


• Frequency distribution


• Central value

Probability Tree

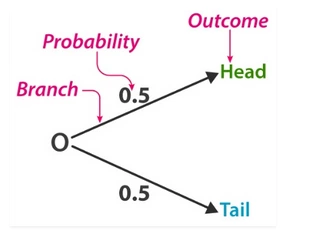
When it comes to organizing and visualizing the different possible outcomes, we take the help of the tree diagram. The two main positions of the tree are branches and ends of the tree. It is on the branch that the probability of each branch is written, where the outcome is present in the ends.  The tree diagram helps in figuring out the conditions on when to add and when to multiply. Do have a look below the tree diagram for the coin.

What are the types of probability?

Students should keep in mind that there are three major types of probabilities which are:

• Theoretical Probability


• Experimental Probability


• Axiomatic Probability

We will now discuss the different types of probability so that you can get the right idea about it:

Theoretical Probability

The theoretical probability is applied based on the possible chances of something to happen. We can take an example that supposes a coin is tossed, then the theoretical probability of getting a head will be ½.

Experimental Probability

The experimental probability is applied based on the observations of an experiment. The calculation is made based on the number of possible outcomes by the total number of trials. Here, we can define with an example that if you toss a coin 10 times, you find that the number of times the heads is recorded is 6 times, then it can be said that the experimental probability for heads is 6/10 or 3/5.

Axiomatic Probability

In the case of axiomatic probability, an axiom or set of rules applies to all types. They are also known as Kolmogorov’s three axioms. It is possible to quantify the chances of occurrence or non-occurrence of the events.

What are Equally Likely Events?

Equally likely events are those that have the same theoretical probability of happening. We can explain this by saying that if a die is thrown, then getting 1/6 would be the probability. In the same way, for all the numbers from 2, 3, 4, 5 and 6, the probability of getting one at a time will be 1/6. Find below some examples of Equally Likely Events when throwing a die:

• Getting an odd number and an even number on a die


• Getting 1, 2 or 3 on rolling a die


• Getting 3 and 5 on throwing a die

So, all the above examples are equally likely events as there are equal probabilities of each event.

What are Complementary Events?

Complementary events are those events where there is a possibility of only two outcomes. It states whether an event is going to occur or not. For example, you may or may not get the job that you have applied for, your friend may or may not visit your house, etc. You can find more examples, such as :

• The student will get promoted to the next class or not.


• It is going to rain or not tonight.


• You will be the winner or not.

Let us now have a look at a solved question:

Question:

There was the tossing of two coins simultaneously 500 times. In the table below, you get the outcomes

Outcome:	Two heads (HH)	One head (HT or TH)	No head (TT)
Frequency:	105	275	120

If the same pair of coins is tossed randomly, then find the probability of getting:

(i) Two heads

(ii) One head

(iii) No head.

Answer:

Given the number of trials = 500

By looking at the data, it is evident that

Number of two heads outcomes (HH) = 105

Number of one head outcome (HT or TH) = 275

Number of no head outcomes (TT) = 120

(i) Probability of getting two heads = favourable outcome of getting 2 heads/ total number of events

     = 105/500

     = 21/100

(ii) Probability of getting one head = favourable outcome of getting 1 head/ total number of events

     = 275/500

     = 11/20

 (iii) Probability of getting no head = favourable outcome of getting no heads/ total number of events

    = 120/500

     = 6/25

Important Chapters:

• NCERT Solution for Maths


• NCERT Solution for Maths Class 7 Chapter Data Handling