Find the center of mass(x,y,z) of the following structure of four identical cubes if the length of each side of a cube is 1 unit.

(1/2,1/2,1/2)
(1/3,1/3,1/3)
(3/4,3/4,3/4)
(1/2,3/4,1/2)
The correct Answer is:C
Ans. (3)
First we find the center of mass of each cube. It is located by symmetry: (0,5,0,5,0,5),(1,5,0,5,0,5),(0,5,1,5,0,5,),(0,5,0,5,1.5)
Now we find the center of mass by treating the COM of each cube as a point particle:
xCOM=0.5+1.5+0.5+0.54=0.75
yCOM=0.5+0.5+1.5+0.54=0.75
zCOM=0.5+0.5+0.5+1.54=0.75
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Knowledge Check
Direction: Read the following Caselet DI carefully and answer the following questions. 3 cubes P, Q, and R are cut from the cubes A, B, and C respectively.
The length of the side of cube P is given by the equation x - 12x + 36 = 0 and the length of the side of cube A is 2 cm more than cube P.
The length of the side of cube Q is given by the equation y + 21y - 46 = 0 and the length of the side of cube B is 3 cm more than cube Q.
The length of the side of cube R is given by the equation z - 10z + 25 = 0 and the length of the side of cube C is 4 cm more than cube R.
Here x, y, and z are in centimeter.
The average length of side of cube P, B, and C is how much percent more or less than the average length of side of cube A, Q, and R?A25% moreB10% lessC33.33% moreD12.5 % moreDirection: Read the following Caselet DI carefully and answer the following questions. 3 cubes P, Q, and R are cut from the cubes A, B, and C respectively.
The length of the side of cube P is given by the equation x - 12x + 36 = 0 and the length of the side of cube A is 2 cm more than cube P.
The length of the side of cube Q is given by the equation y + 21y - 46 = 0 and the length of the side of cube B is 3 cm more than cube Q.
The length of the side of cube R is given by the equation z - 10z + 25 = 0 and the length of the side of cube C is 4 cm more than cube R.
Here x, y, and z are in centimeter.
The average length of side of cube P, B, and C is how much percent more or less than the average length of side of cube A, Q, and R?A25% moreB10% lessC33.33% moreD12.5 % moreDirection: Read the following Caselet DI carefully and answer the following questions. 3 cubes P, Q, and R are cut from the cubes A, B, and C respectively.
The length of the side of cube P is given by the equation x - 12x + 36 = 0 and the length of the side of cube A is 2 cm more than cube P.
The length of the side of cube Q is given by the equation y + 21y - 46 = 0 and the length of the side of cube B is 3 cm more than cube Q.
The length of the side of cube R is given by the equation z - 10z + 25 = 0 and the length of the side of cube C is 4 cm more than cube R.
Here x, y, and z are in centimeter.
What is the ratio of total surface area of cube P to total surface area of cube C?A2:3B5:7C4:9D8:3
A Rubik's cube of edge 3 cm is formed with 27 identical cubes. Find the edge of each identical cube.
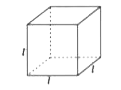
View SolutionA cube is a three-dimensional figure as shown in the given figure. It has six faces and all of them are identical squares. The length of an edge of the cube is given by 1. Find the formula for the total length of the edges of a cube.
View SolutionDirection: Read the following Caselet DI carefully and answer the following questions. 3 cubes P, Q, and R are cut from the cubes A, B, and C respectively.
The length of the side of cube P is given by the equation x - 12x + 36 = 0 and the length of the side of cube A is 2 cm more than cube P.
The length of the side of cube Q is given by the equation y + 21y - 46 = 0 and the length of the side of cube B is 3 cm more than cube Q.
The length of the side of cube R is given by the equation z - 10z + 25 = 0 and the length of the side of cube C is 4 cm more than cube R.
Here x, y, and z are in centimeter.
From the given cubes, which two cubes have equal side length?
View SolutionDirection: Read the following Caselet DI carefully and answer the following questions. 3 cubes P, Q, and R are cut from the cubes A, B, and C respectively.
The length of the side of cube P is given by the equation x - 12x + 36 = 0 and the length of the side of cube A is 2 cm more than cube P.
The length of the side of cube Q is given by the equation y + 21y - 46 = 0 and the length of the side of cube B is 3 cm more than cube Q.
The length of the side of cube R is given by the equation z - 10z + 25 = 0 and the length of the side of cube C is 4 cm more than cube R.
Here x, y, and z are in centimeter.
How many cubes of type A can be made by a cuboid of dimensions 64 cm × 65 cm × 56 cm?
View SolutionDirection: Read the following Caselet DI carefully and answer the following questions. 3 cubes P, Q, and R are cut from the cubes A, B, and C respectively.
The length of the side of cube P is given by the equation x - 12x + 36 = 0 and the length of the side of cube A is 2 cm more than cube P.
The length of the side of cube Q is given by the equation y + 21y - 46 = 0 and the length of the side of cube B is 3 cm more than cube Q.
The length of the side of cube R is given by the equation z - 10z + 25 = 0 and the length of the side of cube C is 4 cm more than cube R.
Here x, y, and z are in centimeter.
What is the ratio of total surface area of cube P to total surface area of cube C?
View Solution
