Taking the data from last problem and assuming that 18% of our body mass is made up of carbon, calculat e the number of beta particles being emitted from the body of a man of mass 50kg in one minute. Assume beta activity due to radiocarbon only.
The correct Answer is:1.41×105 per minute
Step by step video, text & image solution for Taking the data from last problem and assuming that 18% of our body mass is made up of carbon, calculat e the number of beta particles being emitted from the body of a man of mass 50kg in one minute. Assume beta activity due to radiocarbon only. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two radioactive elements A and B are present in a mixture. Both are beta active. Half lives of A and B are 30 minute and 60 minute respectively. The initial activity of the sample hour only 30 beta particles were detected in an interval of 2 second. Assume that law of radioactivity decay is obeyed.
(a) Find the ratio of number of active of A to that of B in the mixture initially.
(b) The molar mass of both A and B is closed to 200g. The mixture contains other substance (non radioactive) aprt from A and B. what fraction of the entire mixure is radioactive (fraction by weight) if it is given what mass of the mixture is 1μg.
View SolutionAn imaginary particle has a charge equal to that of an electron and mass 100 times tha mass of the electron. It moves in a circular orbit around a nucleus of charge + 4 e. Take the mass of the nucleus to be infinite. Assuming that the Bhor model is applicable to this system. (a)Derive an experssion for the radius of nth Bhor orbit. (b) Find the wavelength of the radiation emitted when the particle jumps from fourth orbit to the second orbit.
View Solution
Knowledge Check
In the disintegration of a radioactive element, α- and β-particles are evolved from the nucleus.
.0n1→.1H1+.−1e0+ Antineutrino + Energy
4.1H1→.2He4+2.+1e0+ Energy
Then, emission of these particles changes the nuclear configuration and results into a daughter nuclide. Emission of an α-particles results into a daughter element having atomic number lowered by 2 and mass number by 4, on the other hand, emission of a β-particle yields an element having atomic number raised by 1.
How many α- and β-particle should be emitted from a radioactive nuclide so that an isobar is formed?A1α,1βB1α,2βC2α,2βDnβIn the disintegration of a radioactive element, α- and β-particles are evolved from the nucleus.
.0n1→.1H1+.−1e0+ Antineutrino + Energy
4.1H1→.2He4+2.+1e0+ Energy
Then, emission of these particles changes the nuclear configuration and results into a daughter nuclide. Emission of an α-particles results into a daughter element having atomic number lowered by 2 and mass number by 4, on the other hand, emission of a β-particle yields an element having atomic number raised by 1.
A radioactive element belongs to IIIB group, it emits ona α- and β-particle to form a daughter nuclide. The position of daughter nuclide will be inAIIABIACIIBDIVBWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. If the mass of the particle is m=1.0×10−30kg and α=6.6nm, the energy of the particle in its ground state is closest toA0.8 meVB8 meVC80 meVD800 meV
A particle known as mu mean has a charge equal to that of no electron and mass 208times the mass of the electron B moves in a circular orbit around a nucleus of charge +3e Take the mass of the nucles to be infinite Assuming that the bohr's model is applicable to this system (a)drive an eqression for the radius of the nth Bohr orbit (b) find the value of a for which the redius of the orbit it approninately the same as that at the first bohr for a hydrogen atom (c) find the wavelength of the radiation emitted when the u - mean jump from the orbit to the first orbit
View SolutionFollowing reactions are known as inverse beta decay
p+→v→n+e+
n+v→p+e−
These reactions have extremely low probabilities. Because of this, neutrinos and antineutrinos are able to pass through vast amount of matter without any interaction. In an experiment to detect neutrinos, large number of neutrinos coming out from beta decays of a radioactive material were made to pass through a tank of water, containing a cadmium compound in solution, which provided the protons to interact with antineutrinos, which provided the protons to interact with antineutrinos. Immediately after a proton absorbed a neutrino to yield a positron and a neutron, the positron encountered an electron and both got annihilated. the gamma ray detectors surrounding the tanks responded to the resulting photons. This confirmed that the above reaction has taken place.
(a) How many gamma ray photons are produced when a electron annihilates with a positron? What is energy of each photon? Take the mass of an electron to be 0.00055 u.
(b) The neutron produced in the above reaction was captured by .112Cd to form .113Cd. The atomic masses of these two isotopes of cadmium are are 111.9028u and 112.9044u respectively. mass of a neutron is 1.0087u. find the Q value of this reaction. Assume half of this energy is excitation energ of .113Cd. if the nucleus de-excites by emitting a gamma ray photon find its wavelenght.
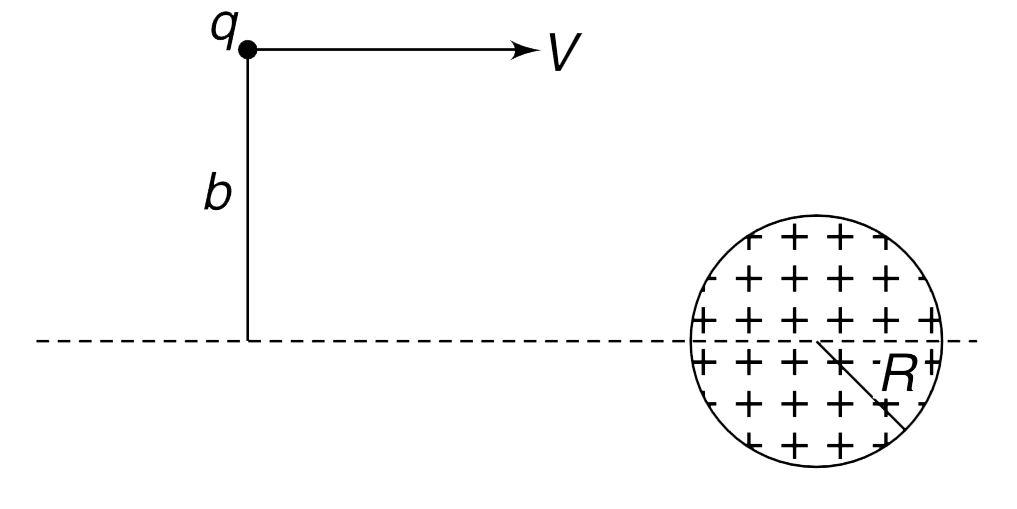
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
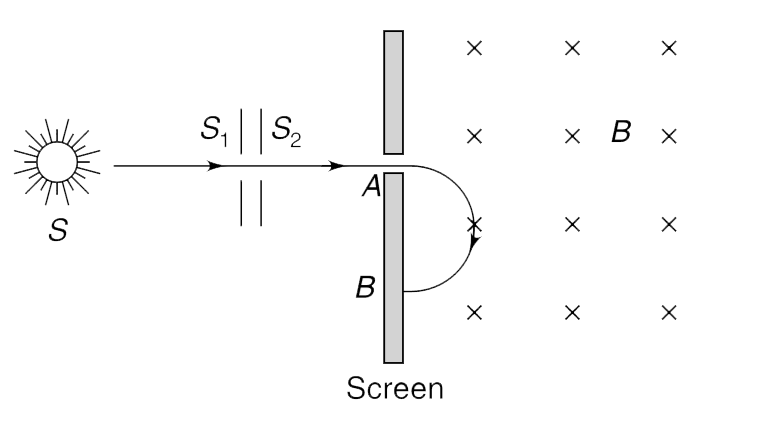
View SolutionA source (s) of beta particles contains a radioactive isotope X. The emitted beta particles are passed through two parallel slits s1 and s2 to get a narrow parallel beam. This beam is made to enter a uniform magnetic field (B). The particles follow semicircular trajectories and are found to hit the screen at all points from A to B the distance AB is equal to 2a. The reaction for decay of a nucleus of X is
X→Y+.0−1e+→v
Calculate the minimum difference in mass of a nucleus of X and Y. mass of an electron is m and charge on it its e.
View SolutionOne way of measuring a person's body fat content is by "weighing" them under water. This works because fat tends to floats on water as it is less dense than water. On the other hand muscle and bone tend to sink as they are more dense. Knowing your 'weight' under water as well as your real weight out of water, the percentage of your body's volume that is made up of fat cab easily be estimated, fat (low density) and everything else (high density). The "weight" measured by spring balance both inside and outside the water. Quotes are placed around weight to indicate that the measurement read on the scales is not your true weight, i.e. the force applied to your body by gravity, but a mersurement of the net downward force on the scale.
A person of mass 165Kg having one fourth of his volume consisting of fat (relative density 0.4) and rest of the volume consisting of everything elese (average relative density 43) is weighed under water by the spring balance. The readibng shown by the spring balance is -
View Solution

