Two rods of equal cross-sections, one of copper and the other of steel are joined to from a composite rod of length 2.0m at 20∘C the length of the copper rod is 0.5m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the length of the component rod also do not change with increase in temperature. Calculate the Young's modulus of steel. Given Young's modulus of copper =1.3×1011N/m2 the coefficient of linear expansion of copper αC=1.6×10−5/.∘c
The correct Answer is:Ys=2.6×1011N/m2αs=0.8×10−5/.∘C
Step by step video, text & image solution for Two rods of equal cross-sections, one of copper and the other of steel are joined to from a composite rod of length 2.0m at 20^(@)C the length of the copper rod is 0.5m. When the temperature is raised to 120^(@)C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the length of the component rod also do not change with increase in temperature. Calculate the Young's modulus of steel. Given Young's modulus of copper = 1.3xx10^(11) N//m^(2) the coefficient of linear expansion of copper alpha_(C) = 1.6xx10^(-5)//.^(@)c by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
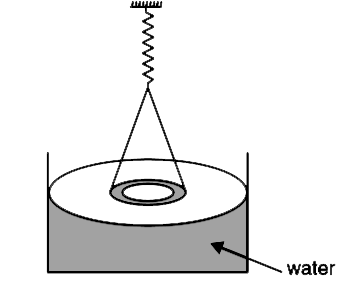
A circular ring has inner and outer radii equal to 10mmand30mm respectively Mass of the ring is m=0.7 g. It gently pulled out vertically from a water surface by a sensitive spring. When the spring is stretched 3.4cm from its equilibrium position the ring is on verge of being pulled out from the water surface. If spring constant is k=0.7Nm–1 find the surface tension of water.
View SolutionDuring a painting process, a thin, flat tape of width b (dimension perpendicular to the plane of the figure) is pulled through a paint filled channel of length L. The density and viscosity of the paint liquid is ρ and η respectively. The tape is pulled at a constant speed v and width of the channel is h. Find the minimum force needed to pull the tape.

View SolutionA composite rod consists of a steel rod of length 25 cm and area 2A and a copper rod of length 50 cm and area A . The composite rod is subjected to an axial load F . If the Young's moduli of steel and copper are in the ratio 2: 1 then
View SolutionTwo rods of equal cross sections, one of copper and the other of steel, are joined to form a composite rod of length 2.0 m at 20∘C, the length of the copper rod is 0.5 m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the lengths of the component rods also do not change with increase in temperature. Calculate Young's modulus of steel. (The coefficient of linear expansion of copper, αc=1.6×10−5∘C and Young's modulus of copper is 1.3×1013N/m2).
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25^(@)C , the composite rod is 1 m long and the copper rod is 30 cm long. At 125^(@)C the length of the composte rod increases by 1.91 mm . When the composite rod is prevented from expanding by bolding it between two rigid walls, it is found that the constituent reds have remained unchanged in length in splite of rise of temperature. Find yong's modulus and the coefficient of linear expansion of the second red (Y of copper =1.3xx10^(10) N//m^(2) and a of copper =17xx10^(-6)//K ).
View SolutionTwo rods of equal cross-sections, one of copper and the other of steel are joined to from a composite rod of length 2.0m at 20∘C the length of the copper rod is 0.5m. When the tempertuare is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is foundthat the length fo the component rod also do not change with increase in temperature. Calcualte the Young's modulus of steel. Given Young's modulus of copper =1.3×1011N/m2 the coefficent of linear expansion of copper αC=1.6×10−5/.∘c
View SolutionWhen composite rod is free, composite rod is free, compositive length increase to 2.002m from temprature 20^(@)C to 120^(@)C . When composite rod is fixed between the support. There is no change in component length. Find Y and alpha of steel if Y_(cu) = 1.5 xx 10^(13 N//m^(2) alpha_(cu) = 1.6 xx 10^(-5//@)C
View Solution_S01_011_Q01.png)
When composite rod is free, then composite length increases to 2.002 m for temperature 20∘C to 120∘C when composite rod is fixed between the support there is no change in component length find y and α of steel, if yc=1.5×1013N/m2αc=1.6×10−5/.∘C.
View Solutionस्टील तथा ताँबे की छड़ की लंबाई क्या होनी चाहिए की सभी तापो पर स्टील की छड़ की लंबाई ताँबे की छड़ से 5 सेमी अधिक रहे | ( ताँबे के लिए α=1.7×10−5 प्रति .∘Cस्टील के लिए 11×10−5प्रति )
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of a different material but of same cross-section. At 25∘C, the composite rod is 1 m in length of which the length of the copper rod is 30 cm. At 125∘C the length of the composite rod increases by 1.91 mm. The coefficient of linear expansion of copper is α=1.7×10−5∘C−1 and that of the second rod is β=n×10−5∘C−1. Find the value of n.
View SolutionA large cylindrical rod of length L is made by joining two identical rods of copper and steel of length (L2) each. The rods are completely insulated from the surroundings. If the free end of copper rod is maintained at 100∘C and that of steel at 0∘C then the temperature of junction is (Thermal conductivity of copper is 9 times that of steel)
View SolutionThe length of a copper rod at 20°C is found to be 150cm when measured with a steel scale which gives correct reading at this temperature.What length of the same copper rod be found when measured with the same rod at 60°C?
View SolutionA composite rod consists of a steel rod of length 25 cm and area 2A and a copper rod of length 50 cm and area A . The composite rod is subjected to an axial load F . If the Young's moduli of steel and copper are in the ratio 2: 1 then
View SolutionTwo rods of equal cross sections, one of copper and the other of steel, are joined to form a composite rod of length 2.0 m at 20^@C , the length of the copper rod is 0.5 m. When the temperature is raised to 120^@C , the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the lengths of the component rods also do not change with increase in temperature. Calculate Young's moulus of steel. (The coefficient of linear expansion of copper, alpha_c=1.6xx10^(-5@)C and Young's modulus of copper is 1.3xx10^(13)N//m^(2) ).
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composte rod increases by 1.91mm. When the composite rod is prevented from expanding by bolding it between two rigid walls, it is found that the constituent reds have remained unchanged in length in splite of rise of temperature. Find yong's modulus and the coefficient of linear expansion of the second red (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composite rod increases by 1.91mm. When the composite rod is prevented from expanding by holding it between two rigid walls, it is found that the constituent rods have remained unchanged in length inspite of rise of temperature. Find young's modulus and the coefficient of linear expansion of the second rod (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View Solution
