Two sources A and B give out sound waves in coherence and in phase. The sources are located at co-ordinates (0,0) and (0,9m) in xy plane. There is a detector located at (40m,0). It was found that the detector records continuous increase in intensity of sound when it is moved in positive y-direction for 4.5m but the intensity was found to fall for some distance when it is moved in negative y direction. What frequency of sound is consistent with these observations? Speed of sound =340ms–1.
The correct Answer is:f<170Hz
Step by step video, text & image solution for Two sources A and B give out sound waves in coherence and in phase. The sources are located at co-ordinates (0, 0) and (0, 9 m) in xy plane. There is a detector located at (40 m, 0). It was found that the detector records continuous increase in intensity of sound when it is moved in positive y-direction for 4.5 m but the intensity was found to fall for some distance when it is moved in negative y direction. What frequency of sound is consistent with these observations? Speed of sound = 340 ms^( –1). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The intensity of a sound wave 20 m away from the sound source is 3nW/m2. Find the intensity of the wave 32 m away from the source, if the half -thickness for sound of this frequency is 120 m.
View SolutionThe intensity of a sound wave 20 m away from the sound source is 3×10−9W/m2. Find the intensity of the wave 32m away from the source, if the half thickness for sound of this frequency is 120m.
View Solution
Knowledge Check
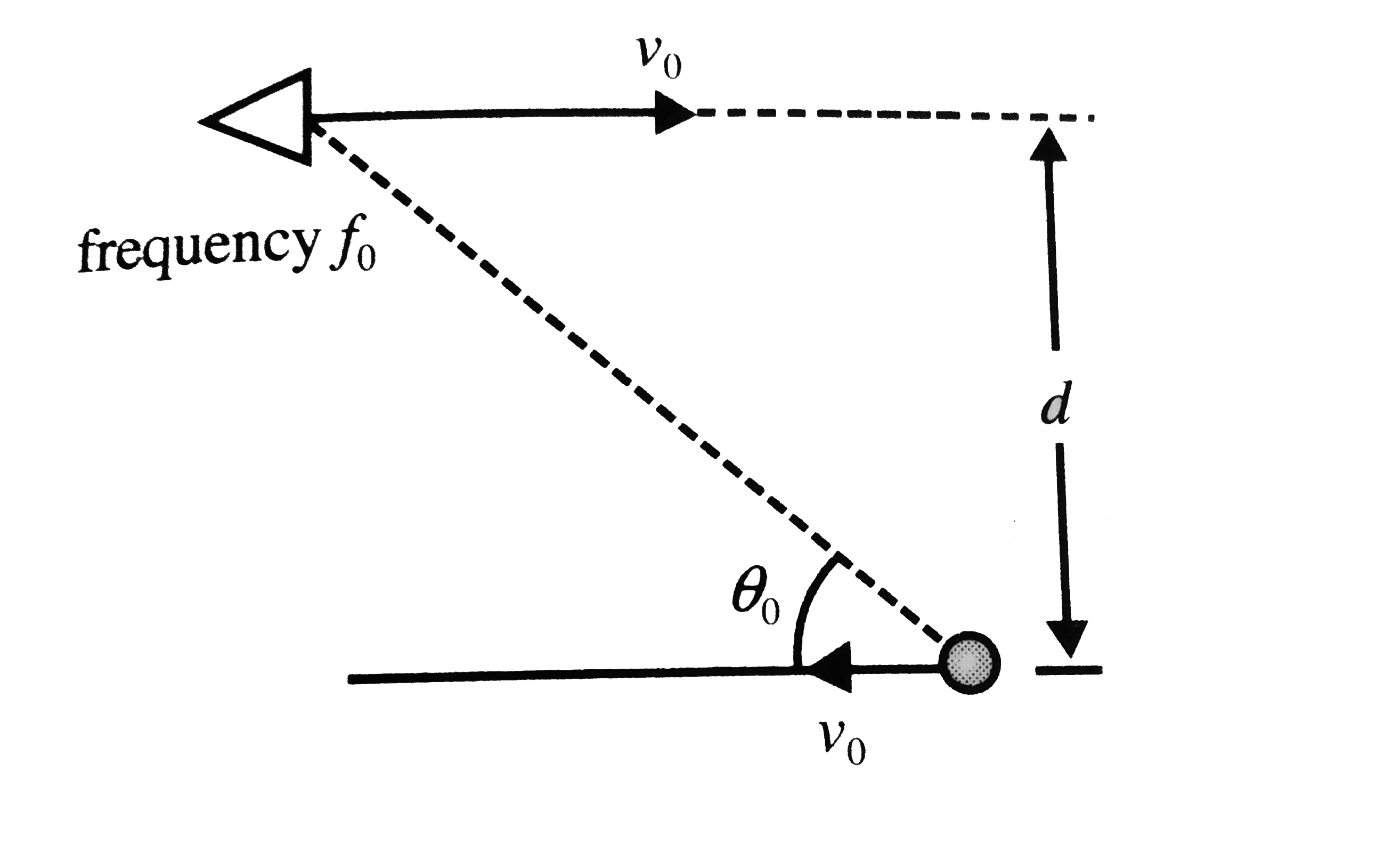
A source of sound and detector are moving as shown in Fig. at t=0. Take velocity of sound wave to be v. For this situation mark out the correct statement(s).AThe frequency received by the detector is always greater than f0BInitially, frequency received by the detector is greater than f0, becomes equal to f0, and then decreases with the time.CFrequency received by the detector is equal to f0 at t=dcotθ0(2v0).DFrequency received by the detector can never be equal to f0The intensity of each coherent source is I0 . Which of the following gives the intensity at a point where the phase difference between the superposing waves is ϕ
AI0(1cosϕ)B2I0cos2(ϕ/2)C2I0(1+cosϕ)DI0cos2(ϕ/2)It is found that what waves of same intensity from two coherent sources superpose at a certain point, then the resultant intensity is equal to the intensity of one wave only. This means that the phase difference between the two waves at that point is
AzeroBπ3C2π3Dπ
Two point sound sources A and B each to power 25πw and frequency 850Hz are 1m apart. The sources are in phase
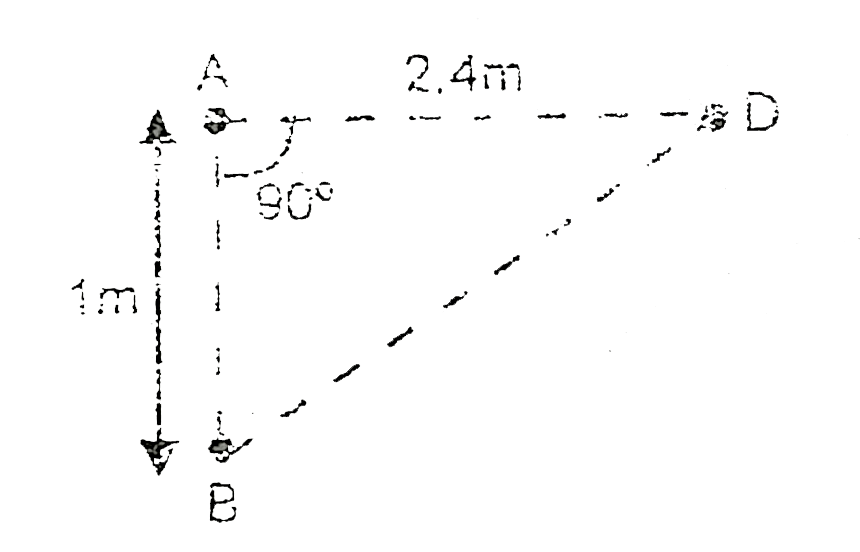
(a) Determine the phase difference between the waves emitting from A and B received by detector D as shown in figure.
(b) Also determine the intensity of the resultant sound wave as recorded by detector D. Velocity of sound =340m/s.
View SolutionThe sound level at a point 5-0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source ?
View SolutionFour sources of sound each of sound level 10dB are sounded together in phase , the resultant intensity level will be (log102=0.3)
View SolutionTwo sources with intensity 4I0 , and 9I0 , interfere at a point in medium. The minimum intensity would be
View SolutionIn Quincke's tube a detector detects minimum intensity. Now one of the tube is displaced by 5 cm. During displacement detector detects maximum intensity 10 times, then finally a minimum intensity (when displacement is complete). The wavelength of sound is :
View Solution

