Two particles A and B of mass 2 m and m respectively attract each other by mutual gravitational force and no other force acts on them. At time t = 0, A was observed to be at rest and B was moving away from A with a speed u. At a later time t it was observed that B was moving towards A with speed u. Assume no collision has taken place by then. Find work done by the gravitational force in the time interval 0 to t
The correct Answer is:mu2
Step by step video, text & image solution for Two particles A and B of mass 2 m and m respectively attract each other by mutual gravitational force and no other force acts on them. At time t = 0, A was observed to be at rest and B was moving away from A with a speed u. At a later time t it was observed that B was moving towards A with speed u. Assume no collision has taken place by then. Find work done by the gravitational force in the time interval 0 to t by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
10 Two particles of masses m1 and m2 initially at rest start moving towards each other under their mutual force of attraction. The speed of the centre of mass at any time t, when they are at a distance r apart, is
View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
Aacceleration of both the particles are equal.Bacceleration of the particle of mass m1 is proportional to m1Cacceleration the particle of mass m1 is proportional to m2.Daccelaration of the particle of mass m1 is inversely proportional to m1.Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
Aaccelerations of both the particles are equal.Bacceleration of the particle of mass m1 is proportional to m1.Cacceleration of the particle of mass m1 is proportional to m2.Dacceleration of the particle of mass m1 is inversely proportional to m1.Two particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
Am1m2vBZeroC(m1−m2)vm1+m2Dm2m1v
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
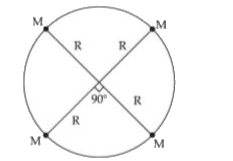
View SolutionTwo particles A and B initially at rest, move towards each other by mutual force of attraction. At the instant when the speed of A is n and the speed of B is 3n, the speed of the centre of mass of the system is
View SolutionTwo particles each of mass M and equidistant from each other move along a circle of radius R under the action of their mutual gravitional attraction the speed of each particle is
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionTwo blocks A and B have masses m and 4m, respectively. Each one is acted upon by a force F. If they acquire the same kinetic energy in time tA and tB, then (tA)/(tB) is
View Solution
