Given that hyperbola $x y - 2 y + 3 x = k$ is tangent to the ellipse $3 x^{2} - 12 x + 2 y^{2} + 12 y + 6 = 0$ at two points A and B On the bases of above answer the following
Length of chord AB of ellipse is

A

$\sqrt{22}$

B

$\sqrt{30}$

C

$\sqrt{40}$

D

$5$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$(x - 2) (y + 3) = k - 6$
$\frac{{(x - 2)}^{2}}{8} + \frac{{(y + 3)}^{2}}{12} = 1$
$x - 2 = X, y + 3 - Y$
$X y = k - 6 \dots . . (1)$

$\frac{X^{2}}{8} + \frac{Y^{2}}{12} = 1 \dots . (2)$
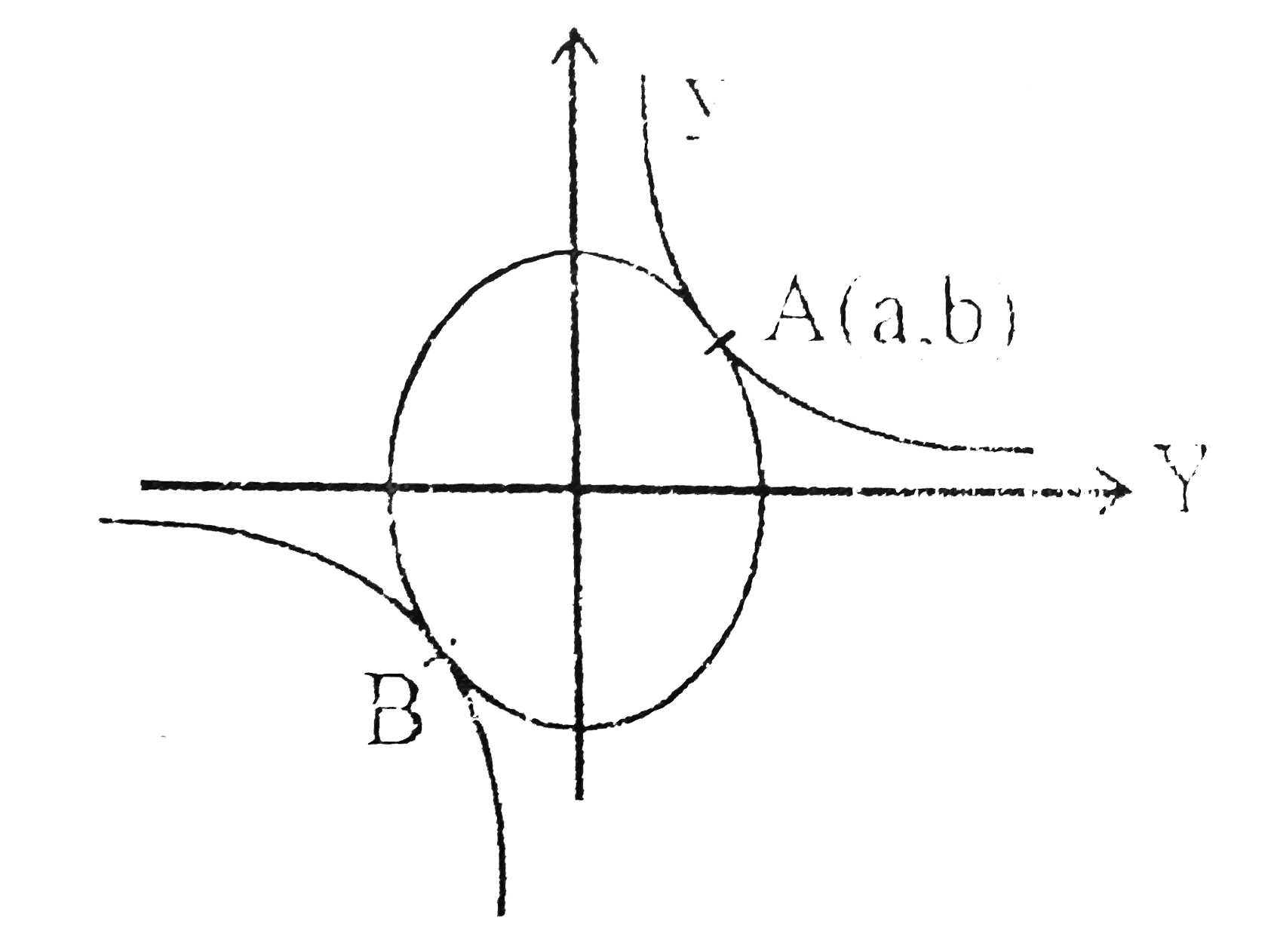
At the point A and B, slopes of tangent to both curves must be equal
$\Rightarrow y^{'} = \frac{β}{α} = \frac{- 3 α}{2 β}$
$2 β^{2} = 3 α^{2}$
since $(α, β)$ satisfies equation (ii)
$\frac{α^{2}}{8} + \frac{β^{2}}{12} = 1$
solving $α = \pm 2, β = \pm \sqrt{6}$
$α, β \in (2, \sqrt{6}) (- 2, - \sqrt{6})$
$α, β \in (2, - \sqrt{6}) (- 2, \sqrt{6})$
$k = 6 + 2 \sqrt{6}$
$k = 6 - 2 \sqrt{6}$
coordinates of tangency
coordinates of tangency
$(4, \sqrt{6} - 3) (0, - \sqrt{6} - 3)$
$(4, - \sqrt{6} - 3) (0, \sqrt{6} - 3)$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Given that hyperbola $x y - 2 y + 3 x = k$ is tangent to the ellipse $3 x^{2} - 12 x + 2 y^{2} + 12 y + 6 = 0$ at two points A and B On the bases of above answer the following
Product of possible values of k is
A $10$
B $12$
C $36$
Dnone of these
Question 2 - Select One
Given that hyperbola $x y - 2 y + 3 x = k$ is tangent to the ellipse $3 x^{2} - 12 x + 2 y^{2} + 12 y + 6 = 0$ at two points A and B On the bases of above answer the following
Product of ordinates of A and B for fixed 'k' is
A $- 6$
B $- 4$
C $3$
Dnone of these
Question 3 - Select One
Centre of the ellipse $3 x^{2} + 4 y^{2} - 12 x - 8 y + 4 = 0$
A(1,1)
B(2,1)
C(3,1)
DNone of these

ALLEN-TEST PAPERS-part-2 Mathematic

Home
Ask Doubt
Profile