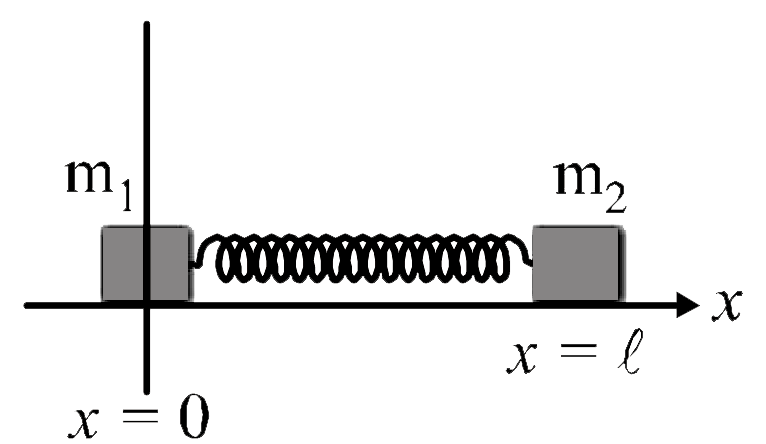
Two masses $m_{1}$ and $m_{2}$ are connected by a massless spring of spring constant k and unstretched length l. The masses are placed on a frictionless straight channel, which are consider our x-axis. They are initially at $x = 0$ and $x = l$ respectively. At $t = 0,$ a velocity $v_{0}$ is suddenly imparted to the first particle. At a later time t, the centre of mass of the two masses is at :

$x = \frac{m_{2} l}{m_{1} + m_{2}}$

$x = \frac{m_{1} l}{m_{1} + m_{2}} + \frac{m_{2} v_{0} t}{m_{1} + m_{2}}$

$x = \frac{m_{2} l}{m_{1} + m_{1}} + \frac{m_{2} v_{0} t}{m_{1} + m_{2}}$

$x = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{m_{1} v_{0} t}{m_{1} + m_{2}}$

Video Solution

Answer

Step by step video & image solution for Two masses m_(1)and m_(2) are connected by a massless spring of spring constant k and unstretched length l. The masses are placed on a frictionless straight channel, which are consider our x-axis. They are initially at x = 0 and x = l respectively. At t = 0, a velocity v_(0) is suddenly imparted to the first particle. At a later time t, the centre of mass of the two masses is at : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

Two masses $m_{1}$ and $m_{2}$ are connected by a massless spring of spring constant k and unstreched length l. The masses are placed on a frictionless straight channel – which we consider our x-axis. They are initially at rest at x = 0 and x = l, respectively. At t = 0, a velocity of v0 is suddenly imparted to the first particle. At a later time t0, the centre of mass of the two masses is at-
A $x = \frac{m_{2} l}{m_{1} + m_{2}}$
B $x = \frac{m_{1} l}{m_{1} + m_{2}} + \frac{m_{2} v_{0} t}{m_{1} + m_{2}}$
C $x = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{m_{2} v_{0} t}{m_{1} + m_{2}}$
D $x = \frac{m_{2} l}{m_{1} + m_{2}} + \frac{m_{1} v_{0} t}{m_{1} + m_{2}}$
Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separately
Bthe magnitude of momentums of each body are equal to each other
Cthe mechanical energy of system remains constant
Dboth (C) and (B) are correct
Two masses $m_{1}$ and $m_{2}$ connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
A $T = 2 π \sqrt{\frac{1}{k} (\frac{m_{1} m_{2}}{m_{1} + m_{2}})}$
B $T = 2 π \sqrt{\frac{1}{k} (\frac{m_{1} + m_{2}}{m_{1} m_{2}})}$
C $T = 2 π \sqrt{(\frac{m_{1}}{k})}$
D $T = 2 π \sqrt{(\frac{m_{2}}{k})}$

DISHA-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-PHYSICS

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :

Two masses m1 and m2 connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-

DISHA-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-PHYSICS

Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :

Two masses $m_{1}$ and $m_{2}$ connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-