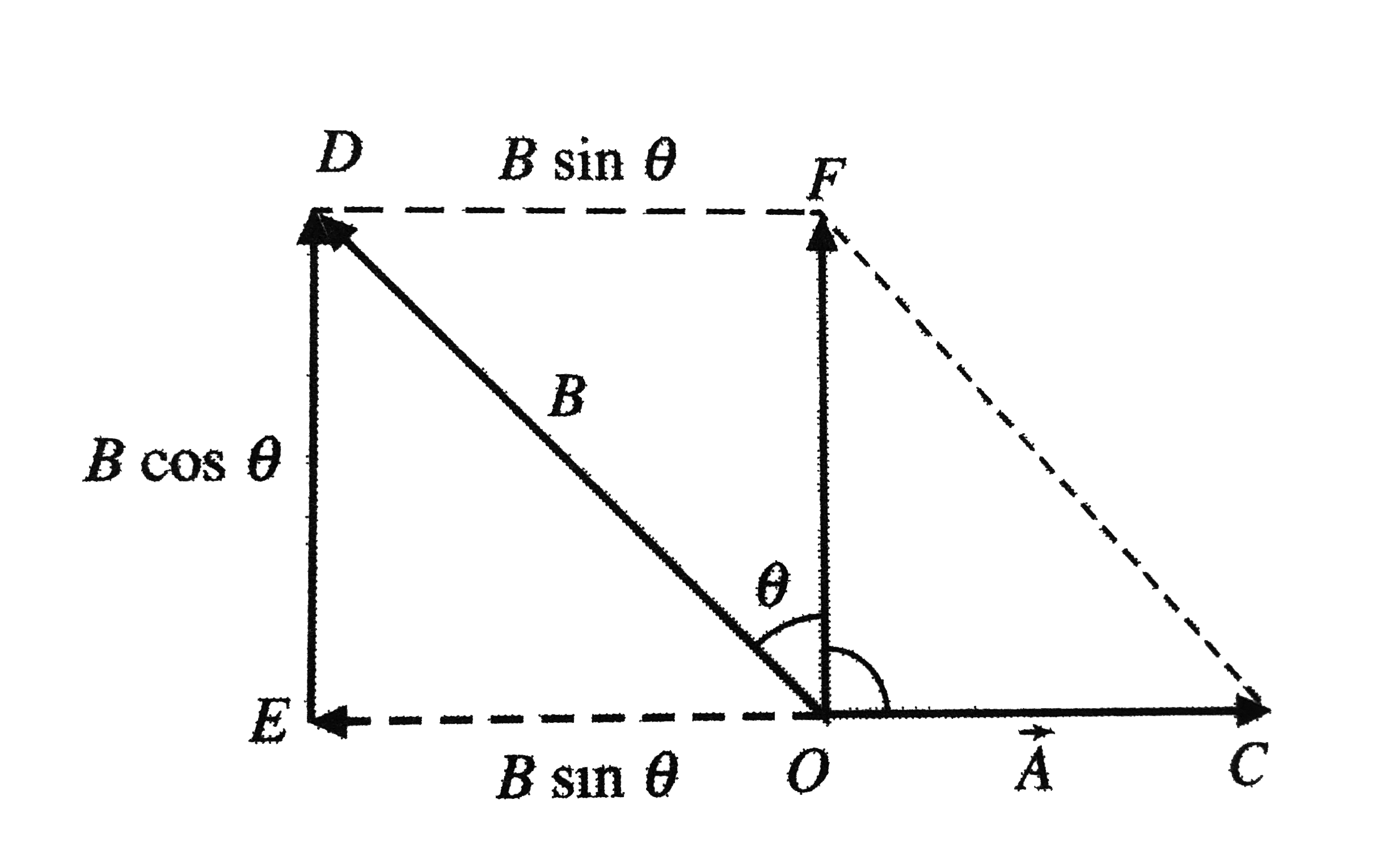
The resultant of two vectors $\to A$ and $\to B$ is perpendicular to the vector $\to A$ and its magnitude is equal to half of the magnitude of the vector $\to B$ . Find out the angles between $\to A$ and $\to B$ .
.

A

$120^{\circ}$

B

$150^{\circ}$

C

$135^{\circ}$

D

$180^{\circ}$

Video Solution

|

Answer

Step by step video & image solution for The resultant of two vectors vecA and vecB is perpendicular to the vector vecA and its magnitude is equal to half of the magnitude of the vector vecB. Find out the angles between vecA and vecB. . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between $\to A and \to B$ is :-
A $120^{\circ}$
B $150^{\circ}$
C $135^{\circ}$
DNone of these
Question 2 - Select One
If for two vector $\to A$ and $\to B$ , sum $(\to A + \to B)$ is perpendicular to the difference $(\to A - \to B)$ . The ratio of their magnitude is
A1
B2
C3
DNone of these
Question 3 - Select One
If for two vector $\to A$ and $\to B$ , sum $(\to A + \to B)$ is perpendicular to the difference $(\to A - \to B)$ . The ratio of their magnitude is
A1
B2
C3
Dnone of these

DISHA-MOTION IN A PLANE-PHYSICS

Home
Ask Doubt
Profile