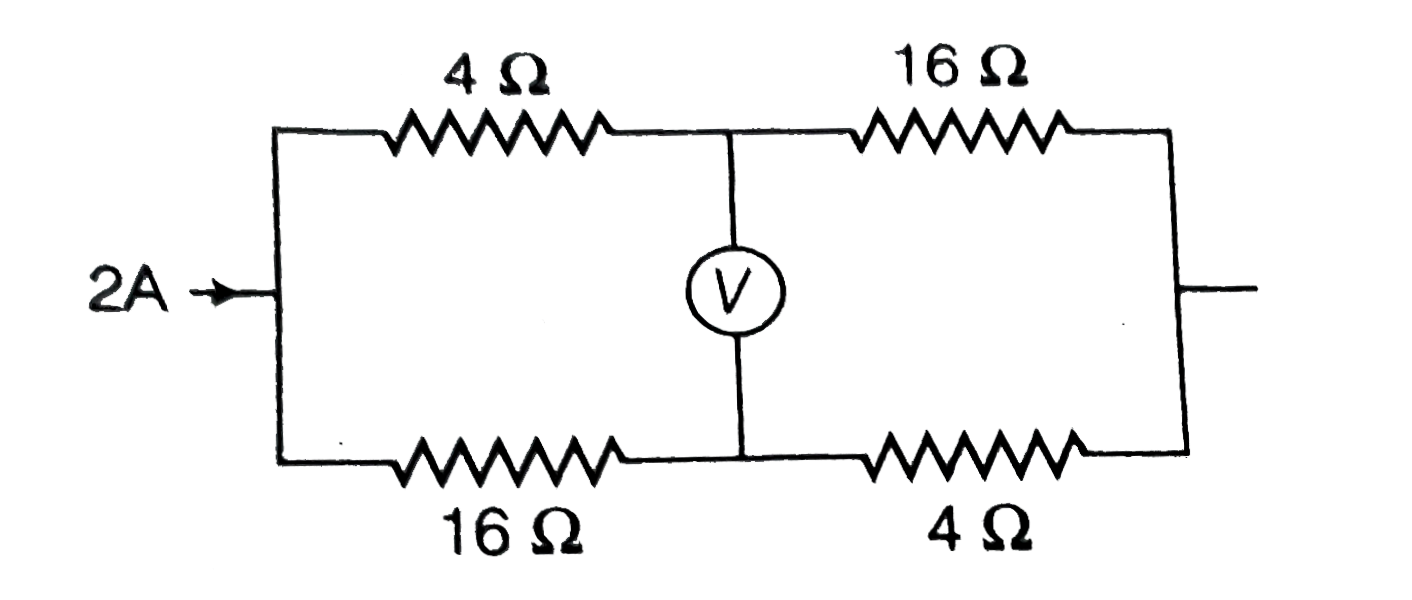
Calculate the reading of voltmeter between X and Y then (Vx−Vy) is equal to -
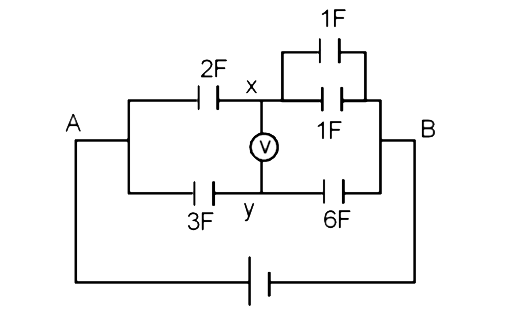
10V
13.33V
3.33V
10.33V
The correct Answer is:C
Step by step video, text & image solution for Calculate the reading of voltmeter between X and Y then (V_(x)-V_(y)) is equal to - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If x, y are the readings of voltmeter and ammeter in Sl units respectively then x + y =
View SolutionIn the circuit shown in the figure, cell is ideal and R2=100Ω. A voltmeter of internal resistance 200Ω reads V12=4VandV23=6V between the pair of points 1−2and2−3 respectively. What will be the reading of the voltmeter between the points 1−3.
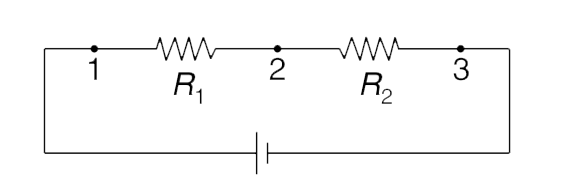
View Solution
Knowledge Check
Find the readings of the ammeter (A) and voltmeter (V):
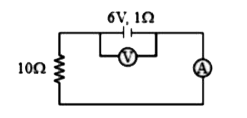 A6 A, 60 VB0.6A, 6VC6A, 6VD611A,6011V
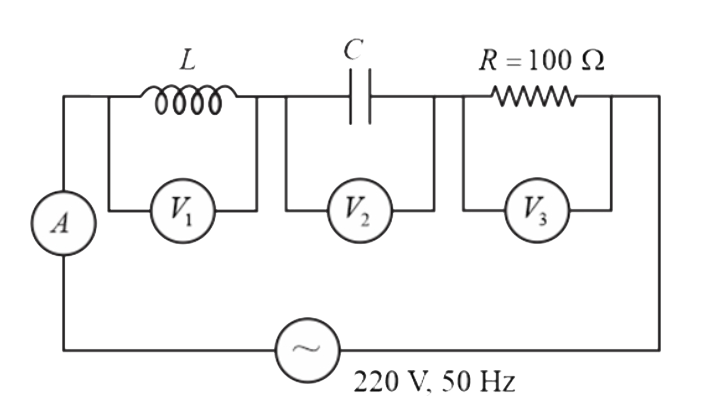
A6 A, 60 VB0.6A, 6VC6A, 6VD611A,6011VIn the given circuit, Fig., the reading of voltmeter V1 and V2 300 votls each. The reading of the voltemeter V3 and ammeter A are respectively
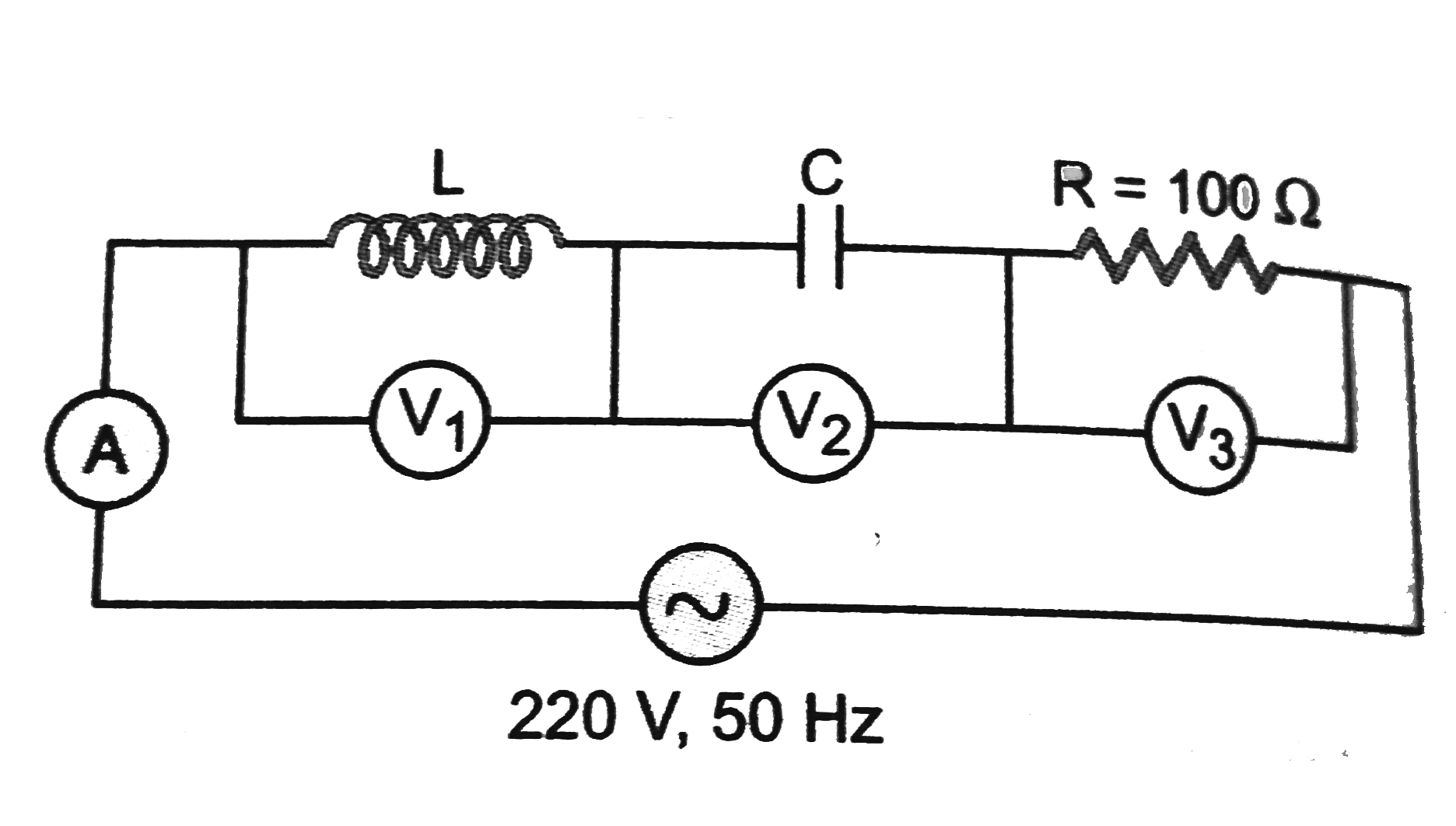 A150V,2.2AB220V,2.2AC220V,2.0AD100V,2.0A
A150V,2.2AB220V,2.2AC220V,2.0AD100V,2.0AA voltmeter reads V volts in an A.C. circuit then V is
Apeak value of the voltageBpeak value of the currentCr.m.s. value of the currentDr.m.s. value of the voltage
In the following circuit reading of voltmeter V is
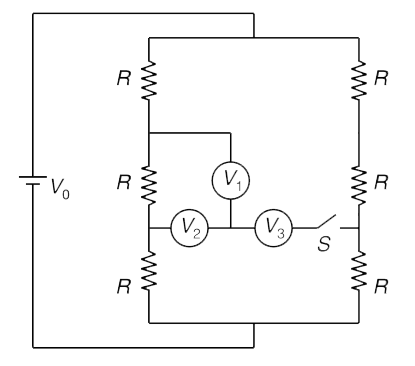
View SolutionIn the circuit shown in figure reading of voltmeter is V1 when only S1 is closed , reading of voltmeter is V2 when only S2 is closed . The reading of voltmeter is V3 when both S1 and S2 are closed then

View SolutionIn the circuit shown in figure all resistances are identical (each equal to R) and the cell has an emf of V0. The three voltmeters V1,V2andV3 are identical and are nearly ideal.
(a) find the reading of the voltmeter V1 when switch ‘S’ is open.
(b) find the reading of the voltmeter V1 after the switch is closed
View SolutionIn the given circuit the reading of voltmeters V1andV2 are 300 volt each . The reading of the voltmeter V3 and ammeter A are respectively
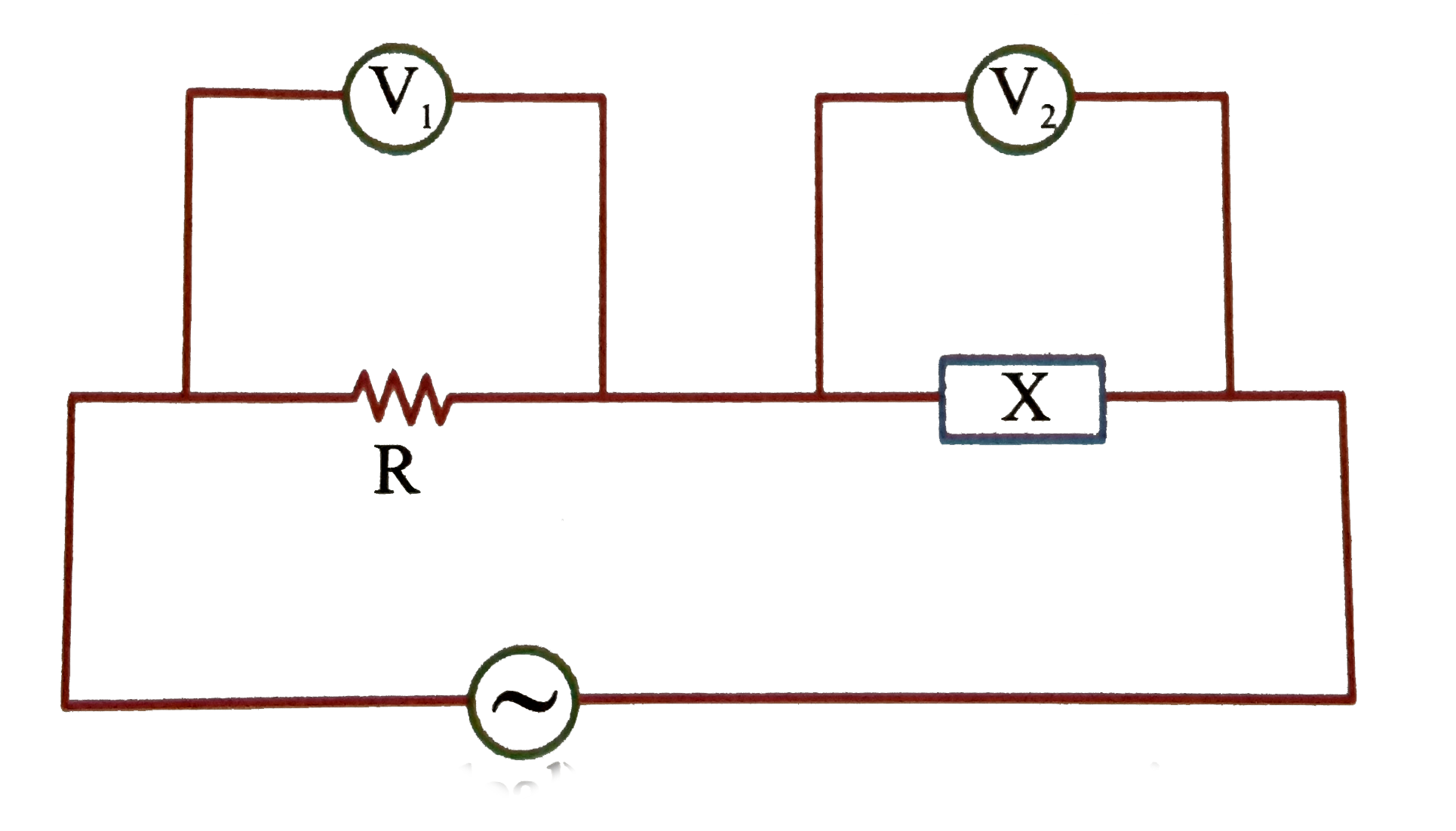
View SolutionIf the reading of the voltmeters vary with time as: V1=20sinωt and V2=−20cos(ωt+π6) then the unknown circuit element x is a:
View Solution
