Statement I : The centre of mass of a circular disc lies always at the centre of the disc.
Statement II : Circular disc is a symmetrical body.
If both Statement- I and Statement- II are true, and Statement - II is the correct explanation of Statement– I.
If both Statement - I and Statement - II are true but Statement - II is not the correct explanation of Statement – I
If Statement - I is true but Statement - II is false.
If Statement - I is false but Statement - II is true
The correct Answer is:A
Step by step video, text & image solution for Statement I : The centre of mass of a circular disc lies always at the centre of the disc. Statement II : Circular disc is a symmetrical body. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Statement I : The centre of mass of a circular disc with uniform mass distribution lies always at the centre of the disc.
Statement II : Circular disc with uniform mass distribution is a symmetrical body.AIf both Statement-I and Statement-II are true, and Statement - II is the correct explanation of Statement– I.BIf both Statement-I and Statement-II are true but Statement - II is not the correct explanation of Statement – I.CIf Statement-I is true but Statement-II is false.DIf Statement-I is false but Statement-II is true.The moment of inertia of a uniform semicircular disc of mass disc through the centre is
A25Mr2B14Mr2C12Mr2DMr2A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
A1/3B1/2C1/6D1/4
Circular Disc and Concentric circles
View SolutionFind the centre of mass of the shaded portion of a disc
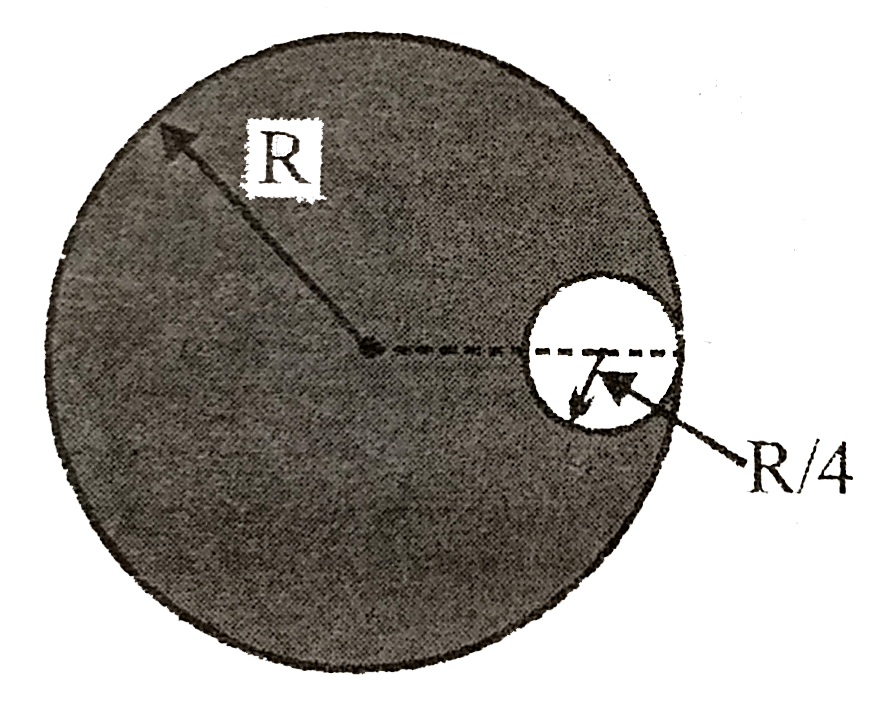
View SolutionFind the centre of mass of the shaded portion of a disc.
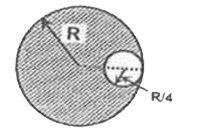
View SolutionA circular disc of radius R is removed from a bigger circular dise of radius such that the circumferences of the discs coincide. The centre of mass of the new disc is αR from the centre of the bigger disc. The value of a is:
View SolutionWhat will be the position of centre of mass of a half disc shown ?
 .
.
View Solution

