In a survey of 1,600 adults in the United States, 48% indicated that television is their primary source of news. The margin of error for the survey is ±2.5%. Which value is outside the interval that is likely to contains the exact percent of all adults in the United States who get the news primarily from telesion?
45
47
49
50
The correct Answer is:A
To solve the problem step-by-step, we will first determine the interval that likely contains the exact percentage of all adults in the United States who get their news primarily from television, based on the given data.
Step 1: Identify the percentage of adults who indicated television as their primary source of news.
The survey indicates that 48% of the adults surveyed indicated that television is their primary source of news.
Hint: Look for the percentage given in the problem statement.
Step 2: Determine the margin of error.
The margin of error provided in the survey is ±2.5%. This means we will add and subtract this value from the percentage found in Step 1.
Hint: Remember that the margin of error gives us a range around the percentage.
Step 3: Calculate the lower limit of the interval.
To find the lower limit, subtract the margin of error from the percentage:
Lower Limit=48%−2.5%=45.5%
Hint: Use subtraction to find the lower boundary of the interval.
Step 4: Calculate the upper limit of the interval.
To find the upper limit, add the margin of error to the percentage:
Upper Limit=48%+2.5%=50.5%
Hint: Use addition to find the upper boundary of the interval.
Step 5: Define the interval.
The interval that is likely to contain the exact percentage of all adults in the United States who get their news primarily from television is:
45.5% to 50.5%
Hint: This interval is formed by the lower and upper limits calculated in the previous steps.
Step 6: Identify which value is outside the interval.
Now, we need to check which of the given options (45, 47, 49, or 50) falls outside the interval of 45.5% to 50.5%.
- 45% is less than 45.5% (outside the interval)
- 47% is within the interval
- 49% is within the interval
- 50% is within the interval
Hint: Compare each option with the interval limits to see if they fall inside or outside.
Conclusion:
The value that is outside the interval is 45%.
Final Answer: 45
The survey indicates that 48% of the adults surveyed indicated that television is their primary source of news.
The margin of error provided in the survey is ±2.5%. This means we will add and subtract this value from the percentage found in Step 1.
To find the lower limit, subtract the margin of error from the percentage:
Lower Limit=48%−2.5%=45.5%
To find the upper limit, add the margin of error to the percentage:
Upper Limit=48%+2.5%=50.5%
The interval that is likely to contain the exact percentage of all adults in the United States who get their news primarily from television is:
45.5% to 50.5%
Now, we need to check which of the given options (45, 47, 49, or 50) falls outside the interval of 45.5% to 50.5%.
- 47% is within the interval
- 49% is within the interval
- 50% is within the interval
The value that is outside the interval is 45%.
Topper's Solved these Questions
Similar Questions
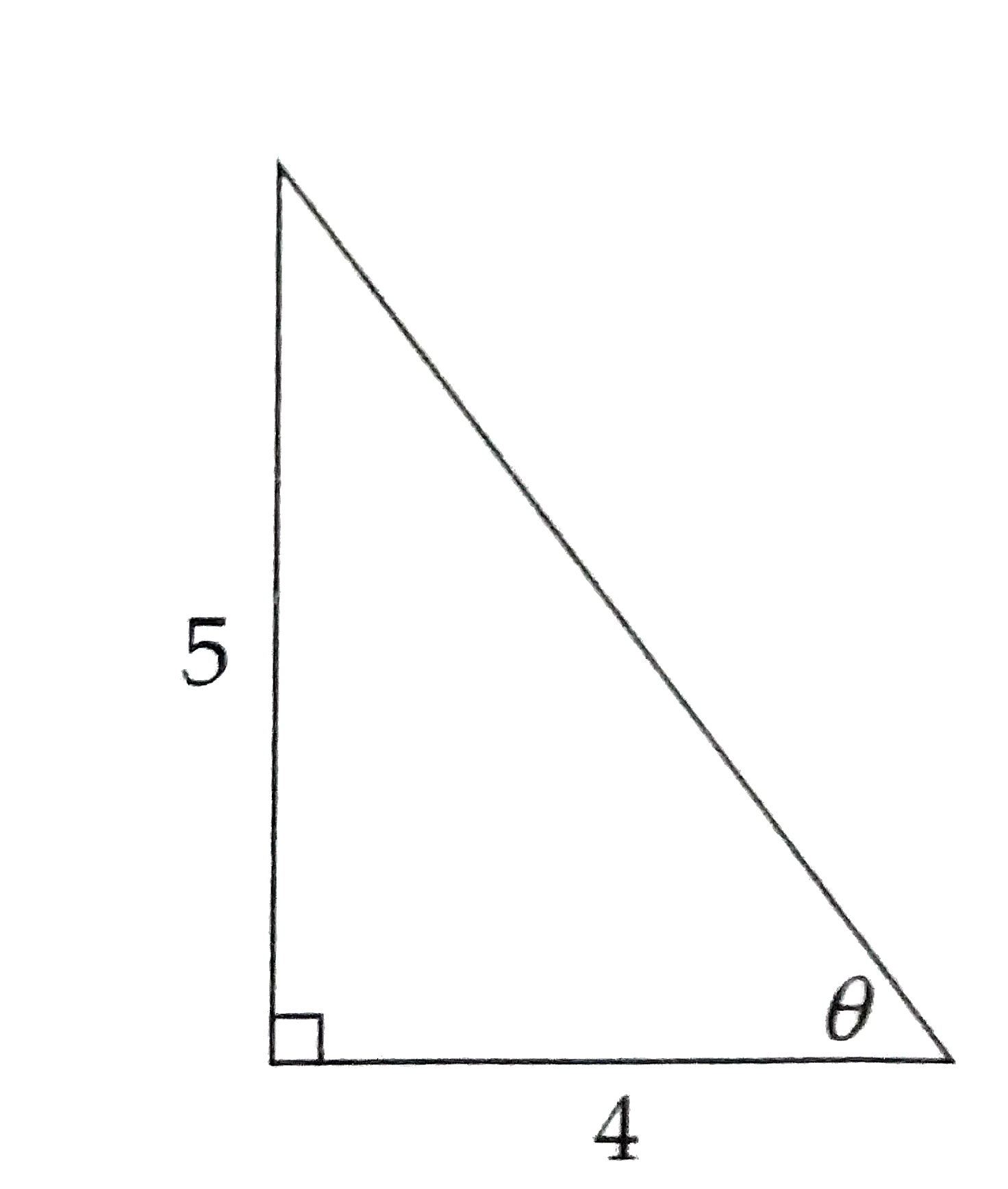
What is the value of θ ?
View SolutionGrowth in human brain from new born to adult is
View SolutionThere is a 'Law' in theory of consumer behaviour which states that as a consumer consumes more and more units of a good, the utility from each new unit consumed :
View Solutionएक सर्वेक्षण में, सर्वेशित लोगों में से 70% के पास कार थी और 75% के पास टी.बी. (टेलीविजन) था| यदि 55% के पास कार और टेलीविज़न दोनों थे, तो सर्वाधिक लोगों में से कितने प्रतिशत के पास कार या टेलीविज़न में से कोई भी नहीं था?
View Solutionएक नगर के सर्वेक्षण से पता चला की सर्वेक्षित लोगों में से, 65% टी.वी. (दूरदर्शन) पर समाचार देखते हैं, 40% समाचार पात्र पढ़ते हैं और 25% समाचार पात्र पढ़ते हैं और टी.वी. (दूरदर्शन) पर भी समाचार देखते हैं| सर्वेशित लोगों में से कितने प्रतिशत न तो समाचार टी.वी. (दूरदर्शन) पर देखते हैं और न ही समाचार पात्र पढ़ते हैं?
View SolutionA political strategist wants to conduct a survey to determine how the likely voters in a given state of 10,000,000 people feel about a politician's stand on an infractructure spending plan. The strategist has a budget to make phone calls to 1,000 people. What would be the most effective approach for him to minimize the margin of error in his survey results?
View SolutionA polling agency recently surveyed 1,000 adults who were selected at random from alargecity and asked each of the adults,“Are you satisfied with the quality of air in the city?”Of those surveyed,78 percent responded that they were satisfied with the quality of air in the city. Based on the results of the survey, which of the following statements must be true?
I. Of all adults in the city,78 percent are satisfied with the quality of air in the city.
II. If another 1,000 adults selected at random from the city were surveyed,78 percent of them would report they are satisfied with the quality of air in the city.
III. If 1,000adults selected at random from a differentcity were surveyed,78percent of them would report they are satisfied with the quality of air in the city
View SolutionStructural unit in adult testis
View Solution(a) What are the source of RBC in embryo and adult man? (b) State the functions of RBC.
View SolutionWhat is the state survey sarva called?
View SolutionWho proposed the 'theory of preformation'i.e.the ovum contains a miniature adult in performed state?
View Solutionस्टेम सैल क्या हैं? एक वयस्क व्यक्ति में स्टेम सैल के दो स्रोत बताइए।
View SolutionGrowth in human brain from new born to adult is
View SolutionGrowth in human brain from new born to adult is
View SolutionWhich was the latest country to be included as a new member state of the United Nations?
View Solution
