Question

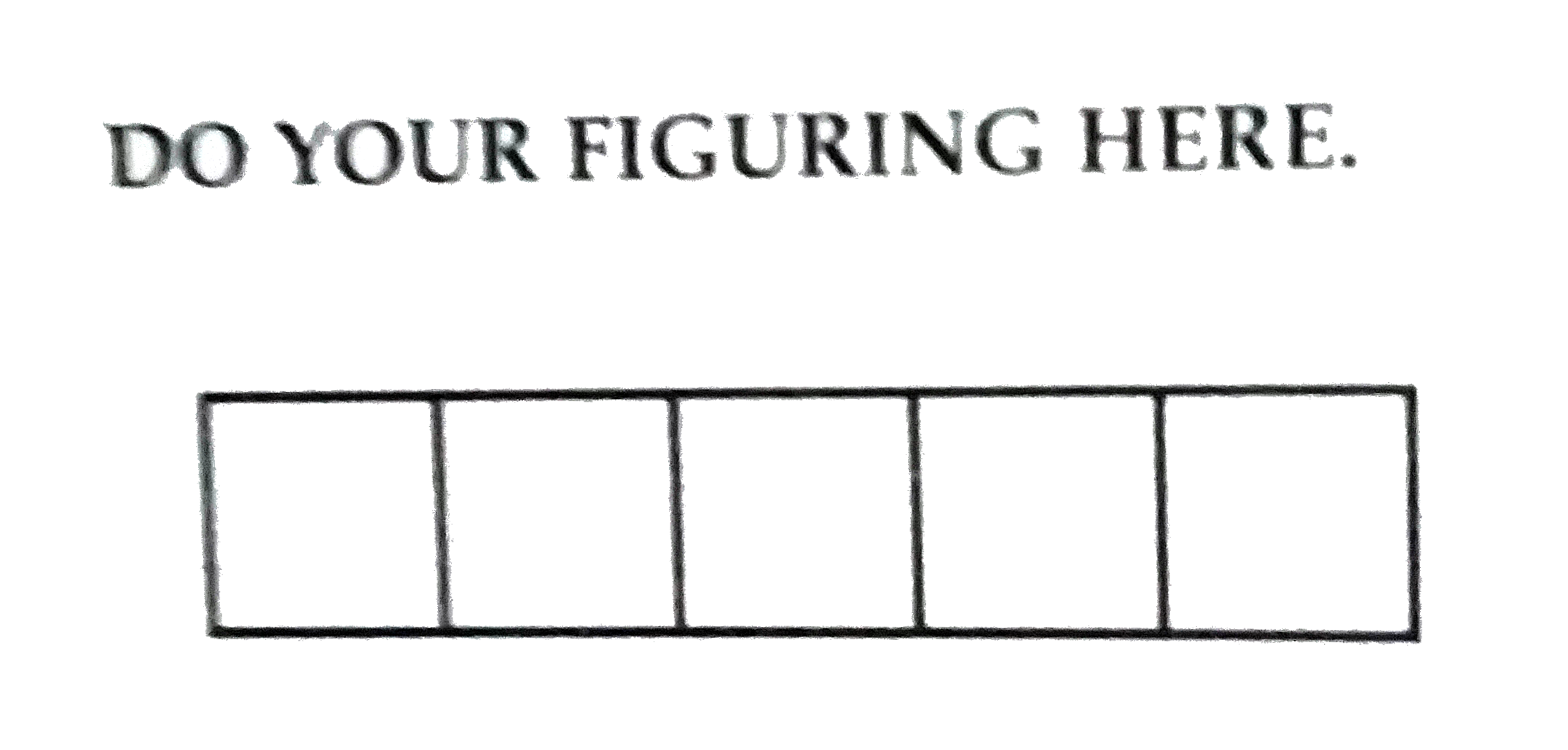
A five - letter code is formed by selecting 5 different letters from the 12 letters A, B, C, D, E, F, G, H, I, J, K, and L and placing these 5 letters in the 5 spaces shown in Figure. Which of the following expressions is the number of different five - letter codes that are possible ?

Options

A. `(12!)/(4!8!)`
B. `(12!)/((5!)(7!))`
C. `(12!)/(7!)`
D. `(12!)/(5!)`

Answer

C

Explanation

The number of five - letter codes possible is the number of ways of permuting 5 different objects from 12 different objects. Say that `._(n)P_(k)` is the number of ways to permute k different objects from n different object, where n is a positive integer and k is an integer such that `0 le k n`. Then `._(n)P_(k)=(n!)/((n-k)!)`. In this question, n = 12 and k =5. The number of possible five - letter codes is `(12!)/((12-5)!)=(12!)/(7!)`
You can solve the question in this way also : Call the space furthest to the left space I , the space adjacent to the space furthest to the left space II , the space in the center space III , the space adjacent to the space furthest to the right space IV , and the space furthest to the right space V. You can place any of the 12 letters in space I. For each of these 12 letters in space I, you can place `12-1=11` letters in space II. For any pair of letters in spaces I and II, you can place `12-2=10` letters in space III. For any triplet of lettes in space IV. For any set of 4 letters in spaces I, II, III and IV, you can place 8 letters in space V. The number of possible five - letter codes is `(12)(11)(10)(9)(8)`. This can be rewritten as `((12)(11)(10)(9)(8)7!)/(7!)` which equals `(12!)/(7!)` matching (C ).