Comprehension # 5
One particle of mass is moving along positive x-axis with velocity . Another particle of mass is moving along y-axis with . At time mass is at and at plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
Co-ordinates of centre of mass where it will stop finally are :-
The correct Answer is:D
To find the coordinates of the center of mass where it will stop finally, we will follow these steps:
Step 1: Identify the initial positions and velocities of the particles
- The first particle (mass m1=1kg) is at position (3m,0) and moving along the x-axis with a velocity of 3m/s.
- The second particle (mass m2=2kg) is at position (0,9m) and moving along the y-axis with a velocity of 6m/s.
Step 2: Calculate the initial position of the center of mass
The position of the center of mass Rcm is given by the formula:
Rcm=m1R1+m2R2m1+m2
Where:
- R1=(3m,0)
- R2=(0,9m)
Calculating Rcm:
Rcm=1⋅(3^i+0^j)+2⋅(0^i+9^j)1+2=(3^i+18^j)3=(1^i+6^j)m
Step 3: Calculate the velocity of the center of mass
The velocity of the center of mass Vcm is given by:
Vcm=m1V1+m2V2m1+m2
Where:
- V1=(3^i,0)
- V2=(0,6^j)
Calculating Vcm:
Vcm=1⋅(3^i+0^j)+2⋅(0^i+6^j)1+2=(3^i+12^j)3=(1^i+4^j)m/s
Step 4: Determine the time until both particles stop
Using the frictional force to find the deceleration:
- For the first particle:
a1=−μm1gm1=−μg=−0.2⋅10=−2m/s2
- For the second particle:
a2=−μm2gm2=−μg=−0.2⋅10=−2m/s2
Using the equation V=U+at:
- For the first particle:
0=3−2t1⟹t1=1.5s
- For the second particle:
0=6−2t2⟹t2=3s
Step 5: Find the distance traveled by each particle until they stop
- For the first particle:
x1=Ut+12at2=3⋅1.5+12⋅(−2)⋅(1.5)2=4.5−1.5=3m
Final position:
R′1=3+3=6m
- For the second particle:
y2=Ut+12at2=6⋅3+12⋅(−2)⋅(3)2=18−9=9m
Final position:
R′2=9+9=18m
Step 6: Calculate the final position of the center of mass
Now we can calculate the final position of the center of mass when both particles stop:
R′cm=m1R′1+m2R′2m1+m2=1⋅(6^i)+2⋅(0^i+18^j)3
Calculating:
R′cm=(6^i+36^j)3=(2^i+12^j)m
Final Answer
The coordinates of the center of mass where it will stop finally are (2m,12m).
---
- The first particle (mass m1=1kg) is at position (3m,0) and moving along the x-axis with a velocity of 3m/s.
- The second particle (mass m2=2kg) is at position (0,9m) and moving along the y-axis with a velocity of 6m/s.
The position of the center of mass Rcm is given by the formula:
Rcm=m1R1+m2R2m1+m2
Where:
- R1=(3m,0)
- R2=(0,9m)
Rcm=1⋅(3^i+0^j)+2⋅(0^i+9^j)1+2=(3^i+18^j)3=(1^i+6^j)m
The velocity of the center of mass Vcm is given by:
Vcm=m1V1+m2V2m1+m2
Where:
- V1=(3^i,0)
- V2=(0,6^j)
Vcm=1⋅(3^i+0^j)+2⋅(0^i+6^j)1+2=(3^i+12^j)3=(1^i+4^j)m/s
Using the frictional force to find the deceleration:
- For the first particle:
a1=−μm1gm1=−μg=−0.2⋅10=−2m/s2
- For the second particle:
a2=−μm2gm2=−μg=−0.2⋅10=−2m/s2
- For the first particle:
0=3−2t1⟹t1=1.5s
- For the second particle:
0=6−2t2⟹t2=3s
- For the first particle:
x1=Ut+12at2=3⋅1.5+12⋅(−2)⋅(1.5)2=4.5−1.5=3m
Final position:
R′1=3+3=6m
y2=Ut+12at2=6⋅3+12⋅(−2)⋅(3)2=18−9=9m
Final position:
R′2=9+9=18m
Now we can calculate the final position of the center of mass when both particles stop:
R′cm=m1R′1+m2R′2m1+m2=1⋅(6^i)+2⋅(0^i+18^j)3
Calculating:
R′cm=(6^i+36^j)3=(2^i+12^j)m
The coordinates of the center of mass where it will stop finally are (2m,12m).
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
The position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
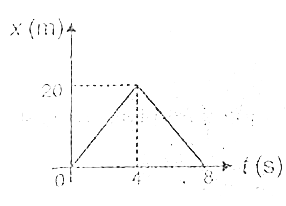
View SolutionA block of mass 1kg is at x=10m and moving towards negative x−aξs with velocity 6m/s. Another block of mass 2kg is at x=12m and moving towards positive x−axis with velocity 4m/s at the same instant. Find position of their centre of mass after 2s.
View Solution
Knowledge Check
Comprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
The centre of mass of the two particles is moving in a straight line which equation is :-Ay=x+2By=4x+2Cy=2x−4Dy=2x+4Comprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
If both the particles have the same value of coefficient of friction μ=0.2. The centre of mass will stop at time t= ..........s :-A1.5B4.5C3.0D2.0A body of mass 1kg is moving along a straight line with a velocity of 1m/s. The external force acting in the body is
A1NB1 dyneC1JDzero
Two particle of mass 1 kg and 2 kg are located at x = 0 and x = 3 m. Find the position of their centre of mass.

View SolutionA particle having mass 2 kg is moving along straight line 3x+4y=5 with speed 8m/s . Find angular momentum of the particle about origin, x and y are in meters.
View SolutionA body A of mass 5kg is moving along the x-axis with a velocity 2m/s. Another body (B) of mass 10 kg is moving along the y-axis with a velocity √3m/s. They collide at the origin and stick together. What is the final velocity of the combined mass?
View SolutionA particle of mass m1=4kg moving at 6ˆims−1perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View Solution
