Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
and
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass is placed over a wedge of mass as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.
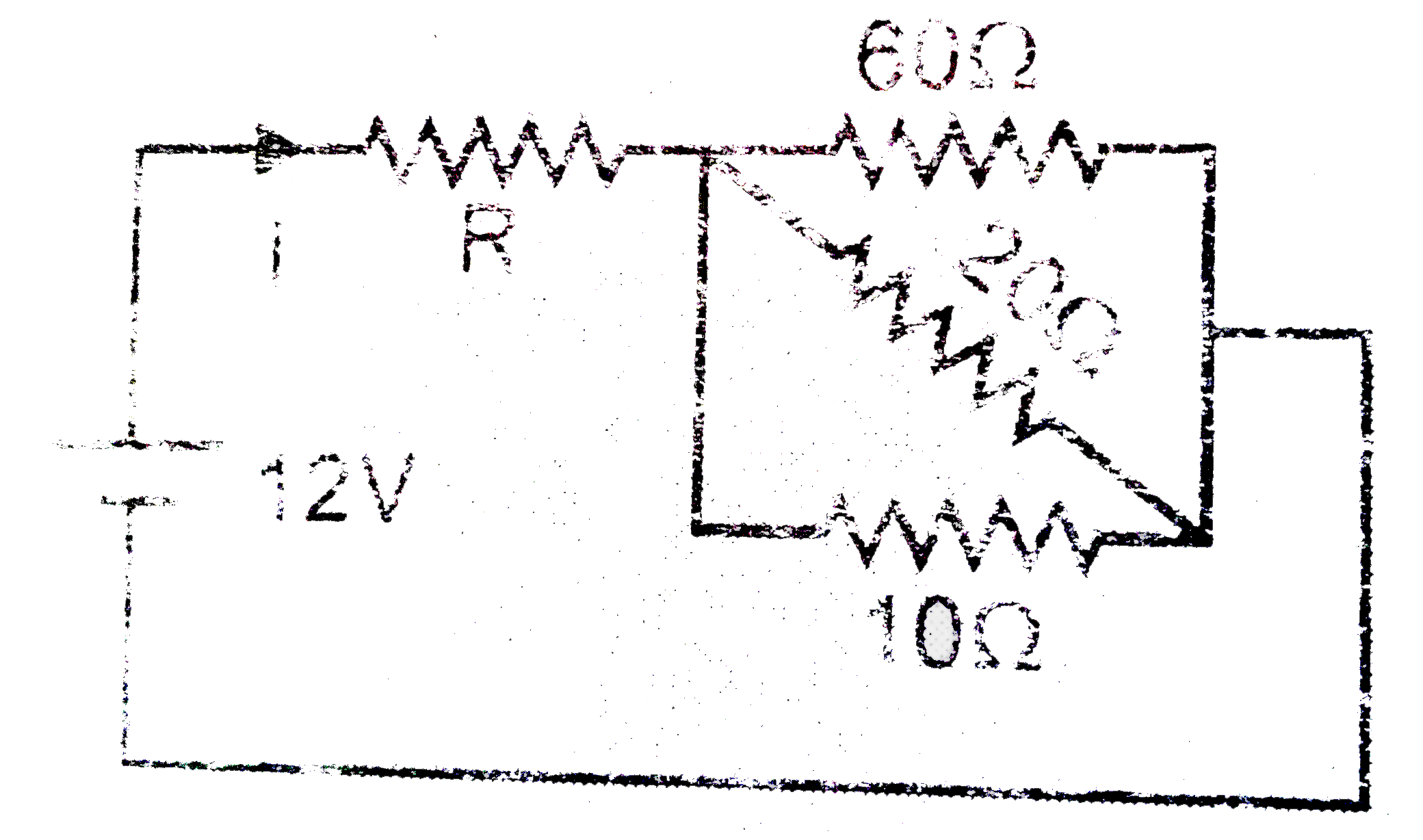
Normal reaction between the two blocks at an instant when absolute acceleration of is at with horizontal is ......... N. Normal reaction at this instant is making with horizontal :-
A
6
B
10
C
4
D
5
Video Solution
Text Solution
The correct Answer is:D
(1)
Newton
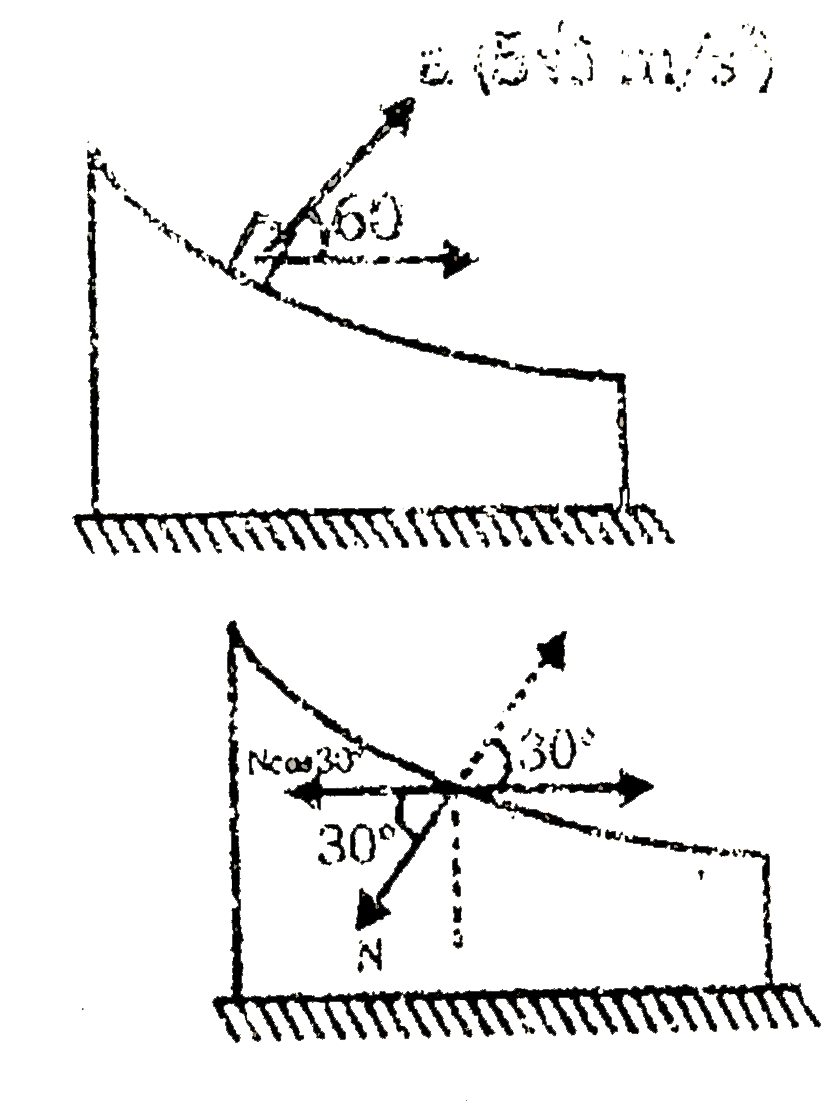
|
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Knowledge Check
Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Final velocity of the wedge is ..........m/s :-A√3B√2C1√2D1√3Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.
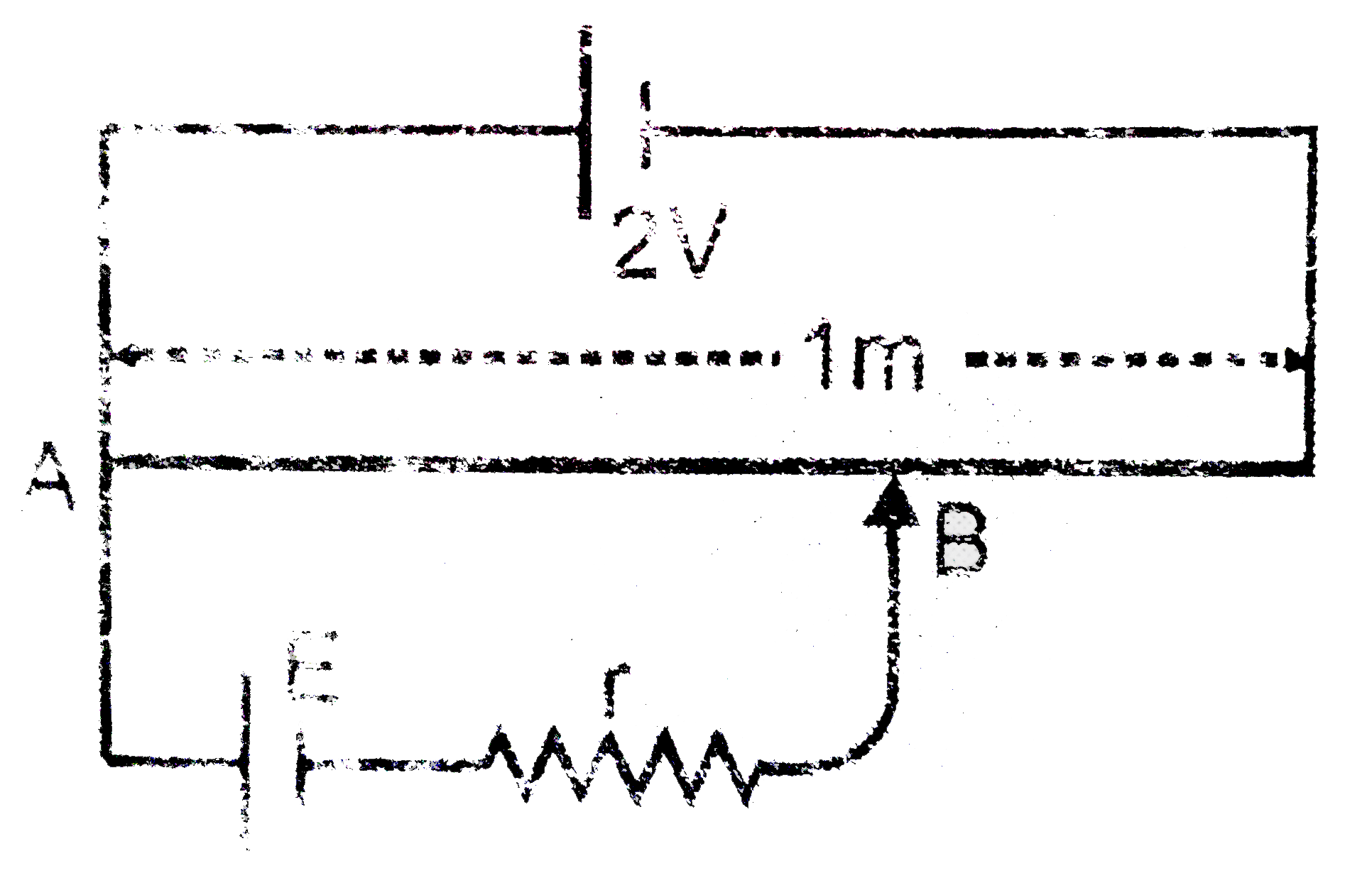
The block will strike the x-axis at x= ............ m :-A4.2B7.6C5.6D6.8Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
ΣmRxR=ΣmLxL,ΣmRvR=ΣmLvL and ΣmRaR=ΣmLaL
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass m=1kg is placed over a wedge of mass M=4kg as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

At the same instant reaction on the wedge from the ground is ........N.A42.5B40C43.46DNone of these
In a potentiometer experiment if the voltage across resistance R and R + r are balanced at the length l1andl2 respectively the value of resistance r will be
View SolutionIf L and R denote the inductance and resistance of a coil respectively, then RL has the dimensions of
View Solution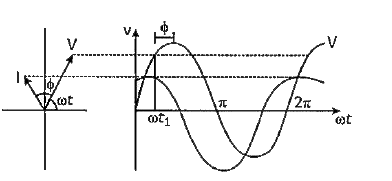
If L= inductance and R = resistance, then the unit of L/R is:
View SolutionIf L and R denote inductance and resistance respectively, then the dimension of L/R is :
View SolutionAn AC source is in series with R and L. if the respective potetntial drops are 200 V and 150 V, the applied voltage will be
View Solution

