Calculate the ratio of intensity of wave train A to wave train B.
_E01_106_Q01.png)
The correct Answer is:1
I∝(AT)2⇒I1I2=(A1A2)2(T2T1)2=(21)2×(12)2=1
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[A]
28 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)
31 Videos
- SEMICONDUCTORSBOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
51 Videos
Similar Questions
Displacement - time graphs for two waves, wave - 1 and wave - 2 are shown here. The ratio of the intensity of wave-1 to that of wave - 2 is
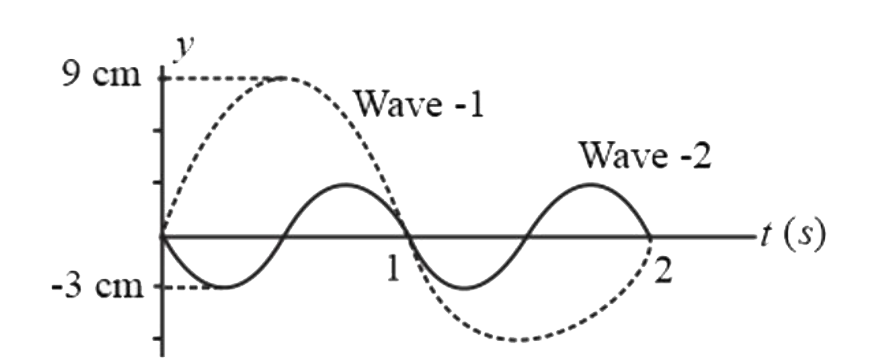
View SolutionTwo waves of intensity ration 1:9 cross eachother at a point. Calculate the ratio of resultant intensities at a point, when (a) waves are incoherent (b) waves are coherent and differ in phase by 60∘.
View Solution
Knowledge Check
The ratio of intensity of wave and energy density gives
AmomentumBtotal energyCpropagation constantDvelocityThe ratio of intensities of two waves is 2. the ratio of intensities of maxima and minima when these waves interfere is approximately
A9B8C34D36If the ratio of intensities of two waves is 1 : 25, then the ratio of their amplitudes will be
A1:25B5:1C26:24D1:5
Two coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
View SolutionIntensity Of The Waves
View SolutionThe ratio of intensities of two waves is 9:16. If these two waves interfere, then determine the ration of the maximum and minimum possible intensities.
View SolutionIf ratio of intensities of two waves is 64 : 9. Calculate the ratio of maximum and minimum intensity in the interference pattern formed by these two waves.
View SolutionThe ratio of intensities of two waves are given by 4:1. The ratio of the amplitudes of the two waves is
View Solution
