A bullet of mass m moving vertically upwards instantaneously with a velocity 'u' hits the hanging block of mass 'm' and gets embedded in it, as shown in the figure. The height through which the block rises after the collision. (assume sufficient space above block) is:
The correct Answer is:C
From momentum conservation
from energy conservation
Topper's Solved these Questions
Similar Questions
Two blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
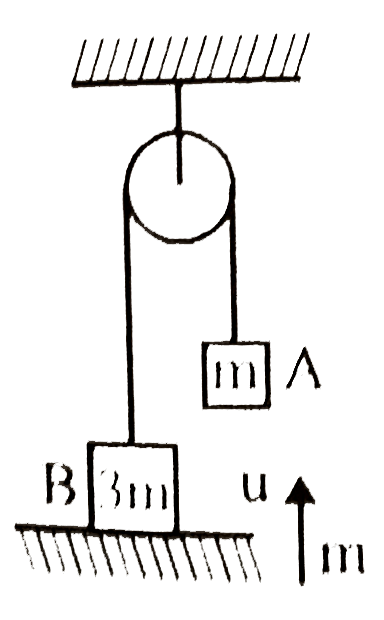
View SolutionA bullet of mass 'm' moving with velocity 'u' passes through a wooden block of mass M=nm as shown in figure. The block is resting on a smooth horizontal floor. After passing through the block, velocity relative to the block is
 .
.
View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2A bullet of mass 'x' moves with a velocity y, hits a wooden block of mass z at rest and gets embedded in it. After collision, the wooden block and bullet moves with a velocity
Axx+zyBx+yxyCzx+yyDx+yzyA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)mD12Mv2×m(m+M)
A bullet of mass m moving horizontally with speed u strikes a suspended wooden block of mass M and gets embedded into it. If block rises to height L2 where L is length of string with which wooden block is connected.The initial velocity(u) of bullet is
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View Solution

