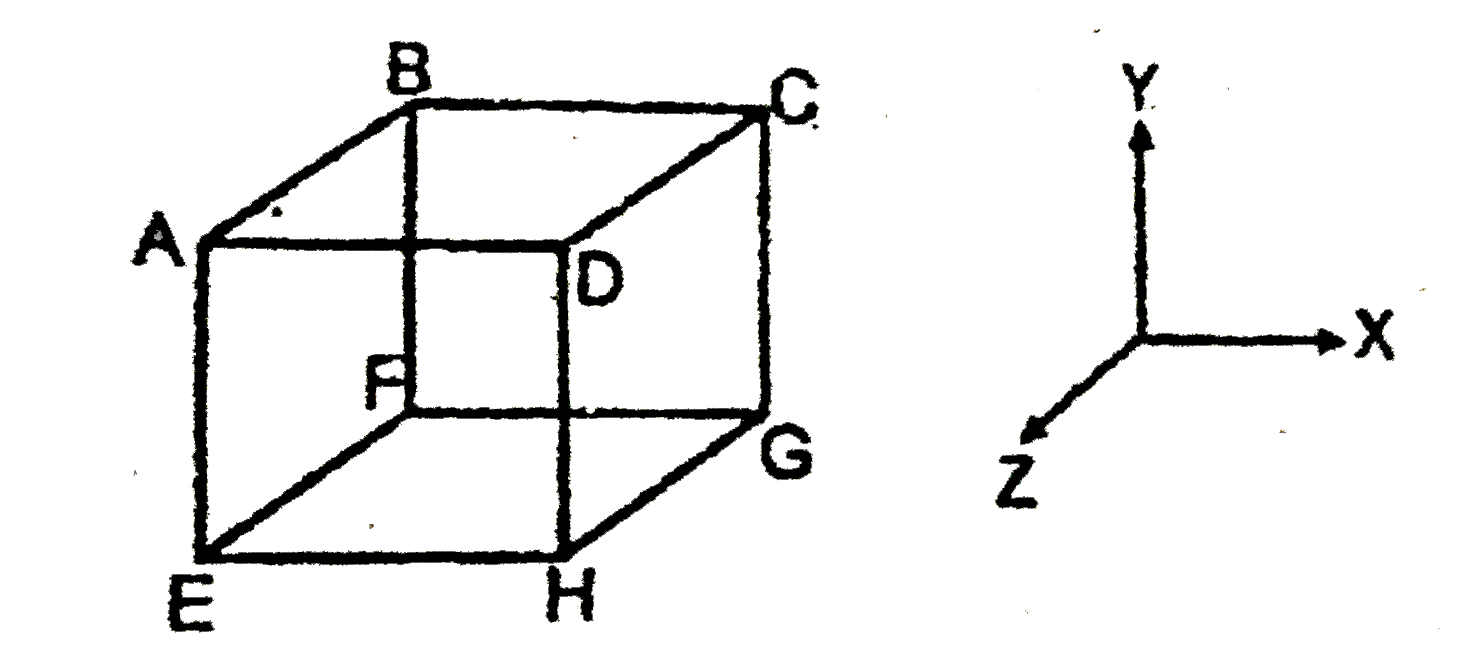
The cubical container ABCDEFGH which is completely filled with an ideal (nonviscous and incompressible) fluid, moves in a gravity free space with a acceleration of a=a0(ˆi−ˆj+ˆk) where a0 is a positive constant. Then the minimum pressure at the point will be
B
C
E
H
The correct Answer is:D
a=a0(ˆi−ˆj+ˆk)
As there is no gravity, the pressure difference will be only due to the acceleration. All points other than point 'B' are acted upon by a pseudo force. Hence, at point 'B' pressure developed is zero.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Examples
22 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise
18 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
A particle moves uniformly with speed v along a parabolic path y=kx2, where k is a positive constant. Find the acceleration of the particle at the point x = 0.
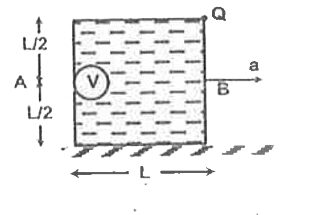
View SolutionA small ball of volume V and density ρ is held inside a cubical container of side L filled with an ideal liquid of density 4ρ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given g=10m/s2
View Solution
Knowledge Check
One mole of an ideal gas undergoes a process in which T=T0+aV3, where T0 and a are positive constants and V is molar volume. The volume for which pressure with be minimum is
A(T02a)1/3B(T03a)1/3Ca(2T0)2/3Da(3T0)2/3A magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
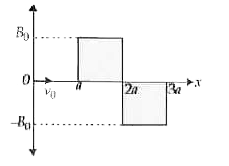
the magnetic field at x=a, The trajectory of the charge in this region can be like,A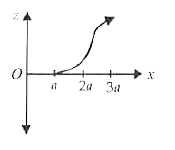 B
B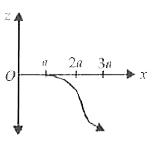 C
C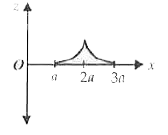 D
D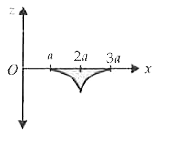
A particle initially (i.e., at t = 0) moving with a velocity u is subjected to a retarding force, as a result of which it decelerates a=−k√v at a rate where v is the instantaneous velocity and k is a positive constant. The time T taken by the particle to come to rest is given by :
AT=2√ukBT=2ukCT=2u3/2kDT=2u2k
A hollow sphere of radius R is filled completely with an ideal liquid of density ρ .Sphere is moving horizontally with an acceleration 2g ,where g is acceleration due to gravity in the space.If minimum pressure of liquid is P0 ,then pressure at the centre of sphere is
View SolutionA particle of charge q>0 is moving at speed v in the +z direction through a region of uniform magnetic field. The magnetic force on the particle →F=F0(3ˆi+4ˆj), where F0 is a positive constant.
(a) Determine the components Bx,By and Bz or at least as many of the three components as is possible from the information given.
(b) If it is given in addition that the magnetic field has magnitude 6F0qv , determine the magnitude of Bz.
View Solution(a) A point moving in a circle of radius R has a tangential component of acceleration that is always n times the normal component of acceleration (radial acceleration). At a certain instant speed of particle is v0. What is its speed after completing one revolution?
(b) The tangential acceleration of a particle moving in xy plane is given by at=a0cosθ. Where a0 is a positive constant and q is the angle that the velocity vector makes with the positive direction of X axis. Assuming the speed of the particle to be zero at x=0, find the dependence of its speed on its x co-ordinate.
View SolutionIn a machine, a fluid from a compressor, which is at high pressure, is allowed to pass through a nozzle. Cross section of the nozzle is shown in the fiuge. The nozzle consists of two sections of radii r1 and r2. The nozzle is fixed on a stand with the help of a clamp. the clamp is a circular ring of radius r1 and width b. The fluid from the compressor is at a presssure of n times the atmospheric pressure p0. assume that the entrie system is horizontal the fluid is ideal and the flow is steady.
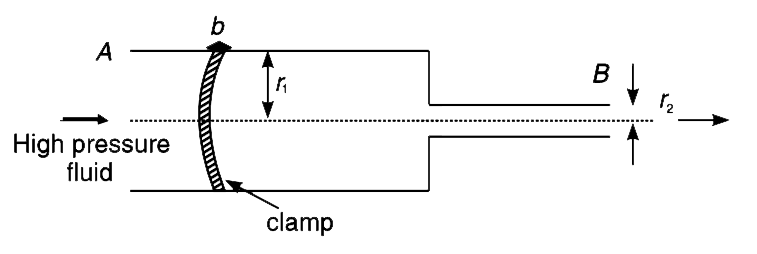
(a) what should be the volume flow rate so that pressure of the fluid at end B reduces to half of its value at end A?
(b) If the entire system is kept in gravity free space and the net force on the nozzle due to the fluid flow is F then determine the minimum radial pressure that should be applied on the clamp. so the nozzle remains in place. Coefficient of friction betwwen clamp and nozzle is μ.
(c) If a small hole is punched anywhere on the thinner part of the nozzle (close to end B) what should be the volume flow rate of the fluid so that it does not gush out?
View SolutionA container contains liquid upto height H and kept on a horizontal frictionless surface .At t=0, the container is given a constant acceleration a0 along positive x-axis.the pressure at point P depends upon :
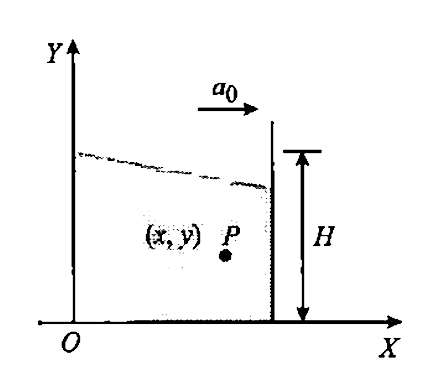
View Solution
