A bullet of mass m=50 gm strikes (Δt≈0)a sand bag of mass M =5 kg hanging from a fixed point, with a horizontal velocity →vp. If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is
10−2
10−3
10−6
10−4
The correct Answer is:D
To solve the problem, we need to determine the ratio of the final kinetic energy to the initial kinetic energy of the bullet after it strikes the sandbag and sticks to it.
1. Identify the masses and initial conditions:
- Mass of the bullet, m=50g=0.050kg
- Mass of the sandbag, M=5kg
- Initial velocity of the bullet, vp (horizontal velocity)
- Initial velocity of the sandbag, vs=0 (since it is hanging and at rest)
2. Apply the conservation of momentum:
Since the bullet sticks to the sandbag, we can use the conservation of momentum before and after the collision:
mvp+Mvs=(m+M)vf
where vf is the final velocity of the bullet and sandbag together.
Plugging in the values:
0.050vp+5⋅0=(0.050+5)vf
Simplifying:
0.050vp=5.050vf
Thus, we can solve for vf:
vf=0.050vp5.050
3. Calculate the initial and final kinetic energies:
- Initial kinetic energy of the bullet:
KEinitial=12mv2p=12(0.050)v2p=0.025v2p
- Final kinetic energy of the bullet and sandbag together:
KEfinal=12(m+M)v2f=12(5.050)v2f
Substituting vf:
KEfinal=12(5.050)(0.050vp5.050)2
Simplifying:
KEfinal=12(5.050)(0.0025v2p25.5025)=0.050v2p2⋅5.050
4. Calculate the ratio of final to initial kinetic energy:
Ratio=KEfinalKEinitial=0.050v2p2⋅5.0500.025v2p
Simplifying this ratio:
=0.0502⋅5.050⋅0.025
=0.0500.2525=50252.5=100505≈0.198
5. Final result:
The ratio of final to initial kinetic energy is approximately 0.198.
- Mass of the bullet, m=50g=0.050kg
- Mass of the sandbag, M=5kg
- Initial velocity of the bullet, vp (horizontal velocity)
- Initial velocity of the sandbag, vs=0 (since it is hanging and at rest)
Since the bullet sticks to the sandbag, we can use the conservation of momentum before and after the collision:
mvp+Mvs=(m+M)vf
where vf is the final velocity of the bullet and sandbag together.
0.050vp+5⋅0=(0.050+5)vf
Simplifying:
0.050vp=5.050vf
Thus, we can solve for vf:
vf=0.050vp5.050
- Initial kinetic energy of the bullet:
KEinitial=12mv2p=12(0.050)v2p=0.025v2p
- Final kinetic energy of the bullet and sandbag together:
KEfinal=12(m+M)v2f=12(5.050)v2f
Substituting vf:
KEfinal=12(5.050)(0.050vp5.050)2
Simplifying:
KEfinal=12(5.050)(0.0025v2p25.5025)=0.050v2p2⋅5.050
Ratio=KEfinalKEinitial=0.050v2p2⋅5.0500.025v2p
Simplifying this ratio:
=0.0502⋅5.050⋅0.025
=0.0500.2525=50252.5=100505≈0.198
The ratio of final to initial kinetic energy is approximately 0.198.
Topper's Solved these Questions
Similar Questions
A bullet of mass m=10 gm strikes a hanging block of mass M=50 gm inelastically, with a horizontal velocity v0=60m/s. Find the change in tension (in N) in the string during collision. Round of to nearest integer. (Take : l=1m)
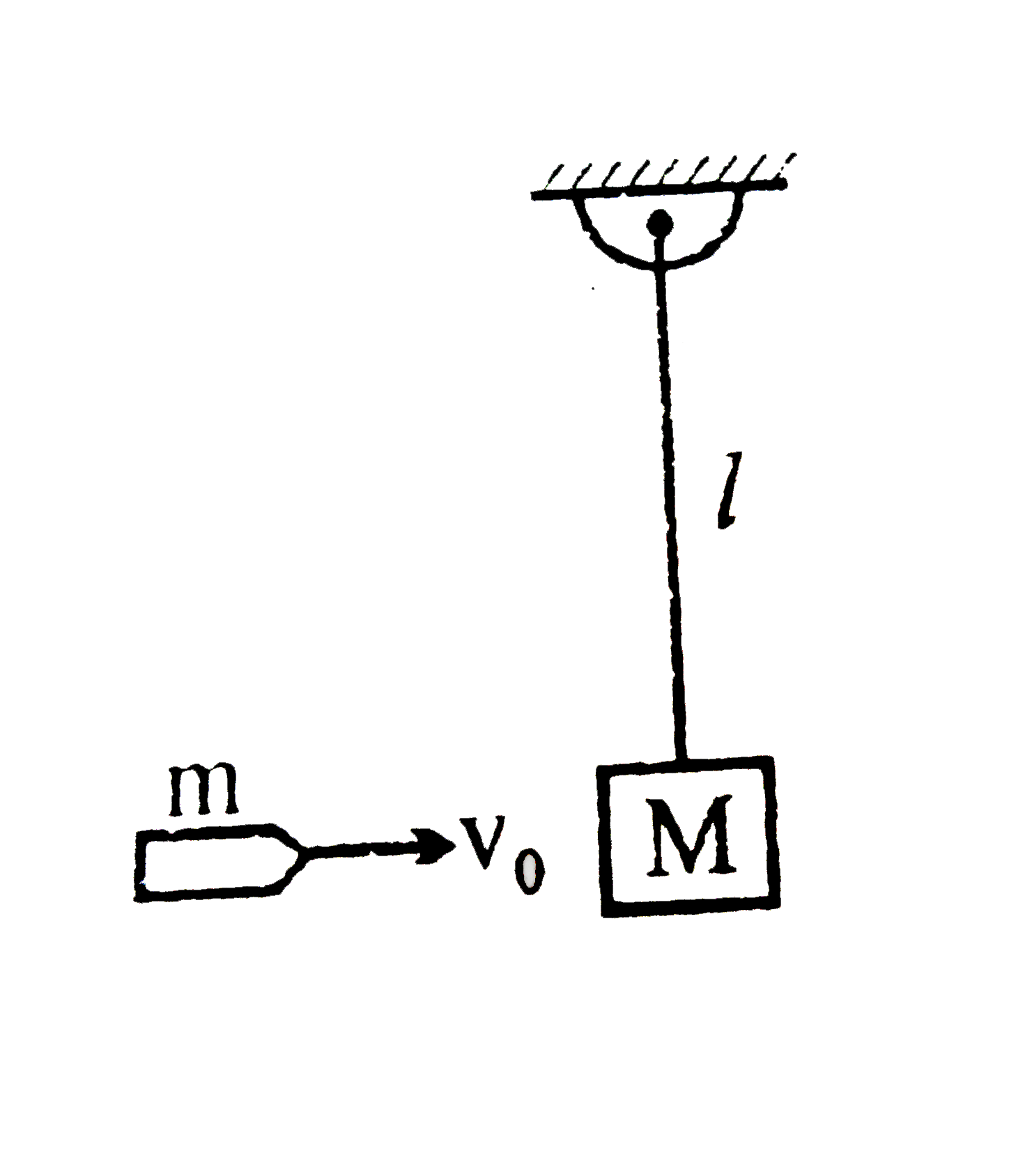
View SolutionA bullet of mass 5 g travels with a speed of 500m/s. If it penetrates a fixed target which offers a constant resistive force of 1000N to the motion of the bullet, find (a) the initial kinetic energy of the bullet (b) the distance through which the bullet has penetrated.
View Solution
Knowledge Check
A bullet of mass m = 50 gm strikes a sand bag of mass M = 5 kg hanging from a fixed point, with a horizontal velocity →vp . If bullet sticks to the sand bag then the ratio of final & initial kinetic energy of the bullet is (approximately) :
A10−2B10−3C10−6D10−4A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass 4.2 gm is moving at certain velocity. If all its kinetic energy liberated is 20 cal, then the initial velocity of the bullet is
A100 m/sB200 m/sC10 m/sD20 m/s
A bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s. If mass of the gun is 4 kg, then calculate the recoil velocity of the gun.
View SolutionA bullet of mass 50 g is fired from a gun with initial velocity of 35 m/s . If mass of the gun is 4 kg , then calculate the recoil velocity of the gun .
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
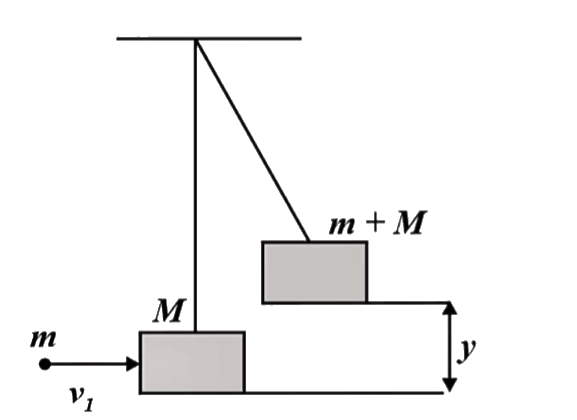
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionA bullet of mass m is fired from a gun of mass M. The recoiling gun compresses a spring of force constant k by a distance d. Then the velocity of the bullet is
View Solution
