If nCx= nCy and x≠y, then x+y=n.
If nCx= nCy
x≠y
So n is 0
Topper's Solved these Questions
Similar Questions
Knowledge Check
If xnyn=(x+y)n,thendydx=
A−1(x−1)2B1(x−1)2C−x(x−1)2Dx(x−1)2
If A=x% of y and B=y% of x,then which of the following is true? a.A is smaller than B b.A is greater than B. c.Relationship between A and B cannot be determined d.If x is smaller than y, then A is greater than B e.None of these
View SolutionIn Figure, ABCD is a trapezium in which AB,DCandDC=40cmandAB=60cm If XandY are, respectively, the mid-points of ADandBC, prove that: ar(traptDCYX)=911,ar(trap(XYBA)
View SolutionProperty (iv) If ^nCx=nCy; then either x=yx=y or x+y=nx+y=n (v) r.nC_r=n. (n-1)C_(r-1)r.nC_r=n. (n-1)C_(r-1)
View SolutionIf x, y>0,(log)yx+(log)xy=103 and xy=144, thenx+y2=√N\ w h e r e\ N is a natural number, find the value of N.
View SolutionLet f, g and h be real-valued functions defined on the interval [0, 1] by f(x)=ex^2+e−x^2, g(x)=xex^2+e−x^2 and h(x)=x2ex^2+e−x^2 . If a,b, and c denote respectively, the absolute maximum of f, g and h on [0, 1], then a=b and c≠b (b) a=c and a≠b a≠b and c≠b (d) a=b=c
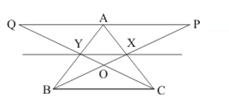
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
View SolutionIf x=5andy=−2thenx−2y=9. The contrapositive of this statement is A.If x−2y=9thenx=5andy=−2 B. If x−2y≠9thenx≠5andy≠−2 C. If x−2y≠9thenx≠5ory≠−2 D. If x−2y≠9the≠itherx≠5andy≠−2
View Solution
