A solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absendce of sliding.
x
The correct Answer is:T=π√3m2k
Step by step video, text & image solution for A solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absendce of sliding. x by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3820videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.399videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3620videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A solid unifom cylinder of mass M performs small oscillations due to the action of two speings, each having stiffness k. The period of these oscillations in absence of any sliding is 2π√xMyK. Find (x+y) (springs have their natural length initially).
'(##CEN_KSR_PHY_JEE_C16_E01_021_Q06##)'View SolutionA small block oscillates back and forth on as smooth concave surface of radius R figure. Find the time period of small oscillation.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform cylinder of mass m and radius R is in equilibrium on an inclined plane by the action of a light spring of stiffness k, gravity and reaction force acting on it. If the angle of inclination of the plane is ϕ, then angular frequency of small oscillations of the cylinder is...........
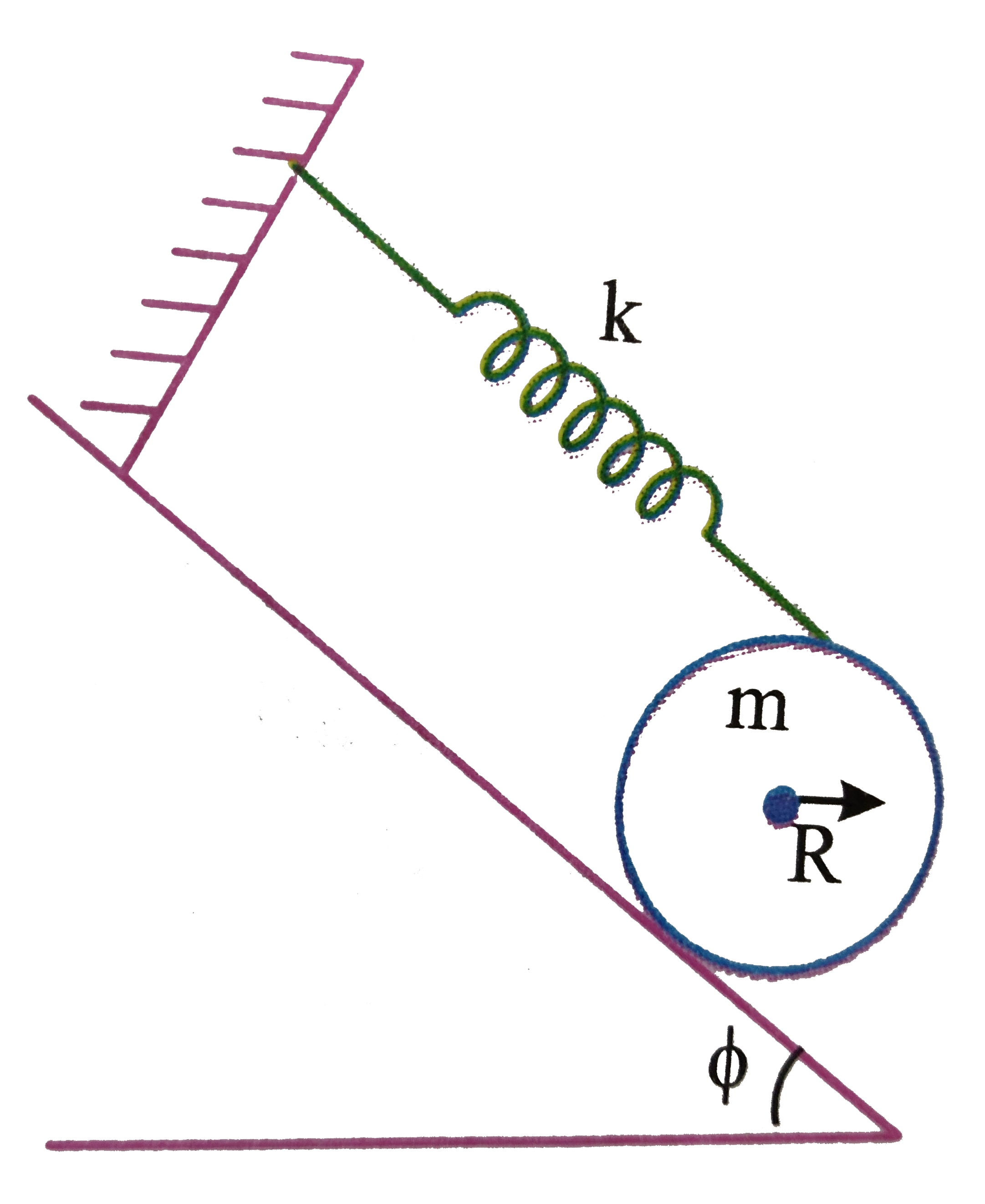 A2√kmB2√2kmC2√2k3mD√2km
A2√kmB2√2kmC2√2k3mD√2km - Question 2 - Select One
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK - Question 3 - Select One
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A solid uniform cylinder of mass M performs small oscillations in horizontal plane if slightly displaced from its mean position shown in figure. If it is given that initially springs are in natural lengths and cylinder does not slip on ground during oscillaitons due to frications between ground and cylinder. Force constant of each spring is k.
Find time period of these oscillation.
_S01_027_Q01.png) View Solution
View SolutionA uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffness, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder
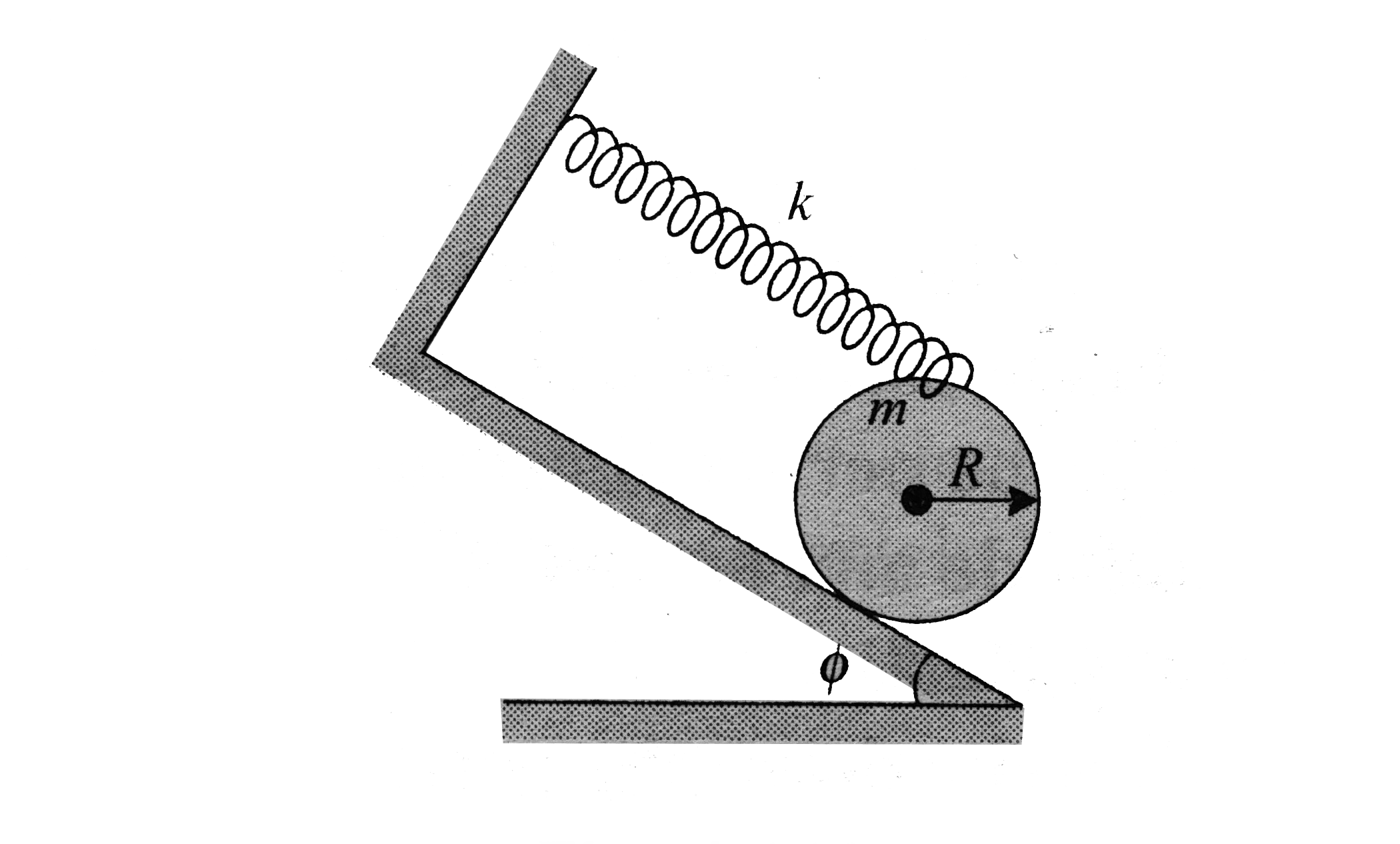 View Solution
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
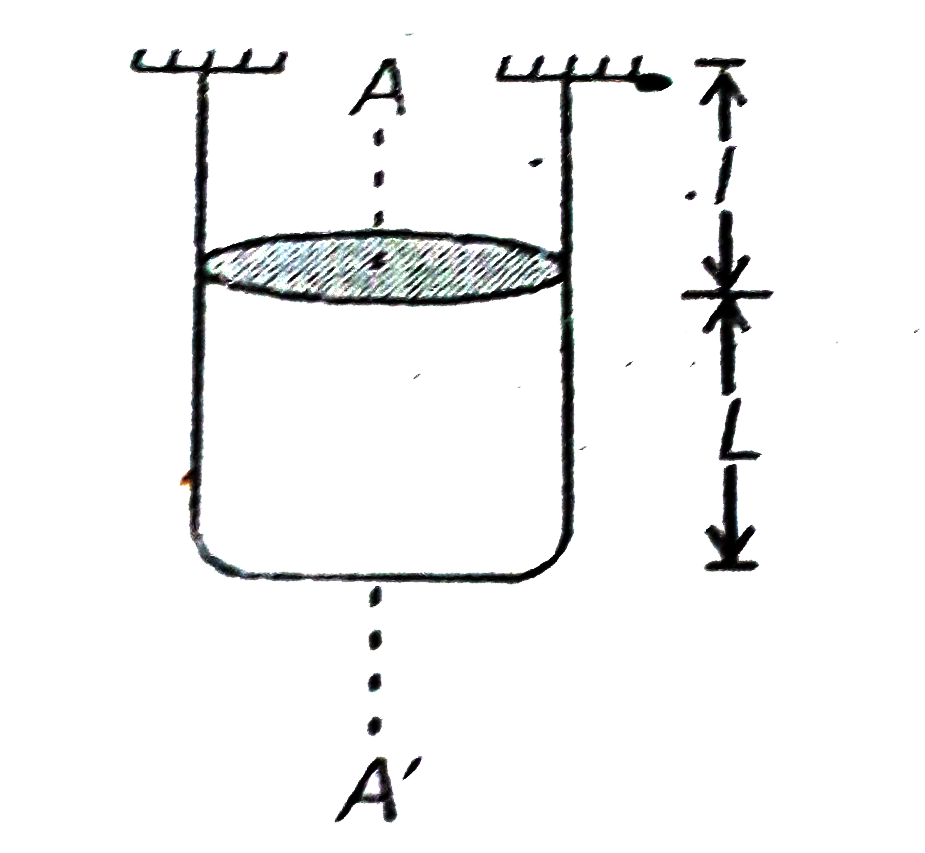 View Solution
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView SolutionA uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
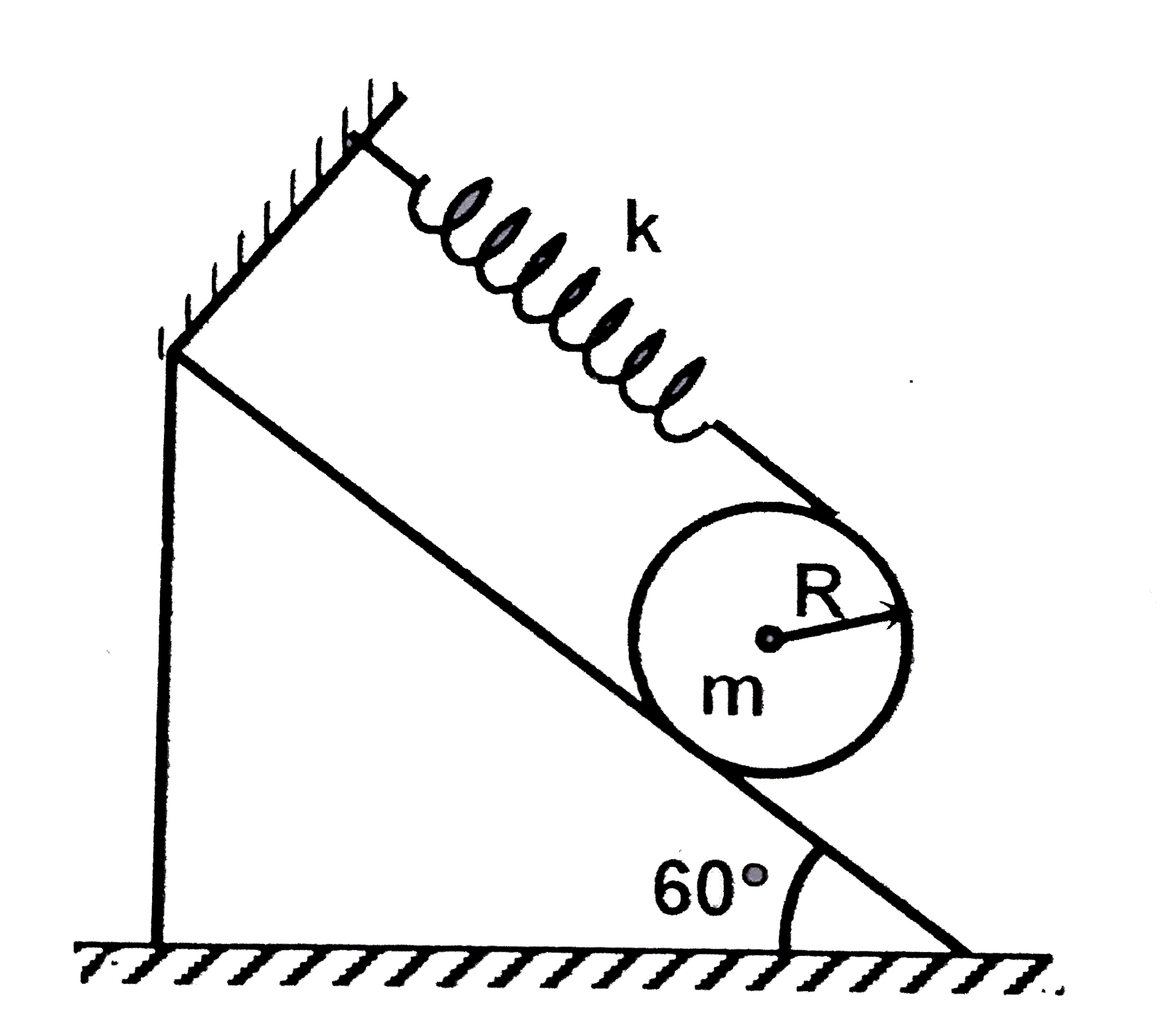 View Solution
View Solution

