A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.

Time taken to cover the distance in above part is :
(√2+14√2)sec
(√2−14√2)sec
14√2sec
18sec
The correct Answer is:C
t=xvA=14√2sec
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.21
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.22
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.19
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions

Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling . The rod is of mass 'm' and has another weight of mass 2 m hung at a distance of 75 cm from A . The tension in the string at A is :
View SolutionA stick of length L=2.0m is leaned against a wall as shown. It is released from a position when θ=60∘. The end A of the stick remains in contact with the wall and its other end B remains in contact with the floor as the stick slides down. Find the distance travelled by the centre of the stick by the time it hits the floor.

View Solution
Knowledge Check
A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.

Minimum magnitude of relative velocity of A with respect to B during the motino specified in question 5 is :A2m/sB4m/sC6m/sDnone of theseA meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.
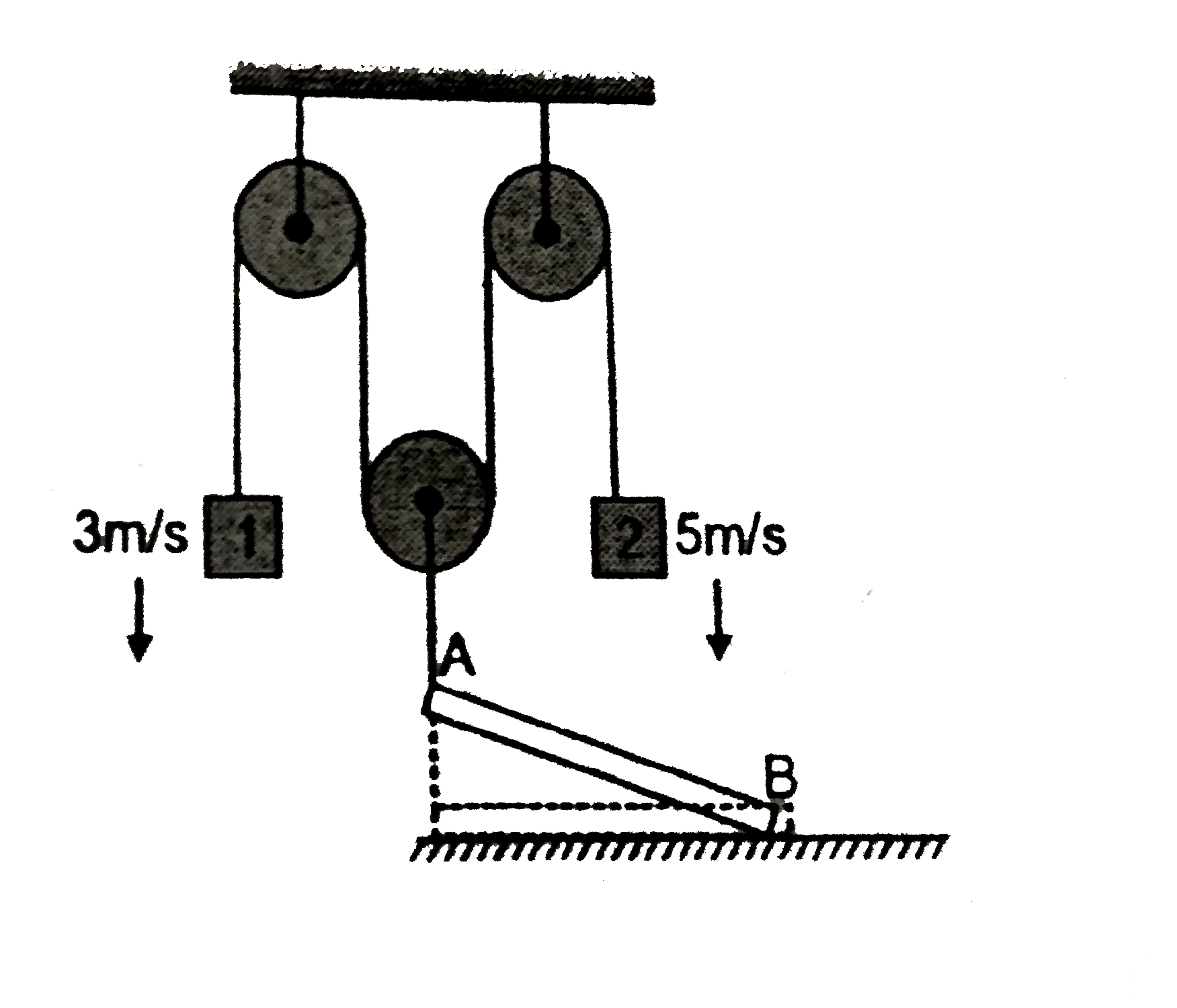
If block 1 and 2 are given constant speeds as shown then the distance moved by end B over the floor in the period for which speed of B is less than A.A(√2+1√2)mB(√2−1√2)mC1√2mD12mTwo identical blocks are attached by a massless string running over a pulley as shown in figure. The rope initially runs over the pulley at its (the rope's) midpoint, and the surface that block 1 rests on is frictionless. Blocks 1 and 2 are initially at rest when block 2 is released with the string taut and horizontal. Assume that the initial distance from block 1 to the pulley is the same as the initial distance from block 2 to the wall.
 ABlock 1 hits the pulley before Block 2 hits the wayBBlock 2 hits the wally before block 1 hits the pulleyCblock 1 hits pulley simultaneously with block 2 hitting the wallDwhich block hits the obstruction first depends on the actual mass of the blocks and its length of the sring
ABlock 1 hits the pulley before Block 2 hits the wayBBlock 2 hits the wally before block 1 hits the pulleyCblock 1 hits pulley simultaneously with block 2 hitting the wallDwhich block hits the obstruction first depends on the actual mass of the blocks and its length of the sring
A stick of length L is dropped from a high tower. An ant sitting at the lower end of the stick begins to crawl up at the instant the stick is released. Velocity of the ant relative to the stick remains constant and is equal to u. Assume that the stick remains vertical during its fall, and length of the stick is sufficiently long.

(a) Calculate the maximum height attained by the ant measured from its initial position.
(b) What time after the start the ant will be at the same height from where it started?
View SolutionTwo blocks A and B having masses m1=1kgm2=4kg are arranged as shown in the figure The pulleys P and Q are light and frictionless. All the blocks are resting on a horizontal floor and the pulleys are held such that strings remains just taut. At moment t=0 a force F=30 t (N) starts acting on the pulley P along vertically upward direction as shown in the figure The time when the blocks A and B loose contact with ground is 4/x sec then x is:
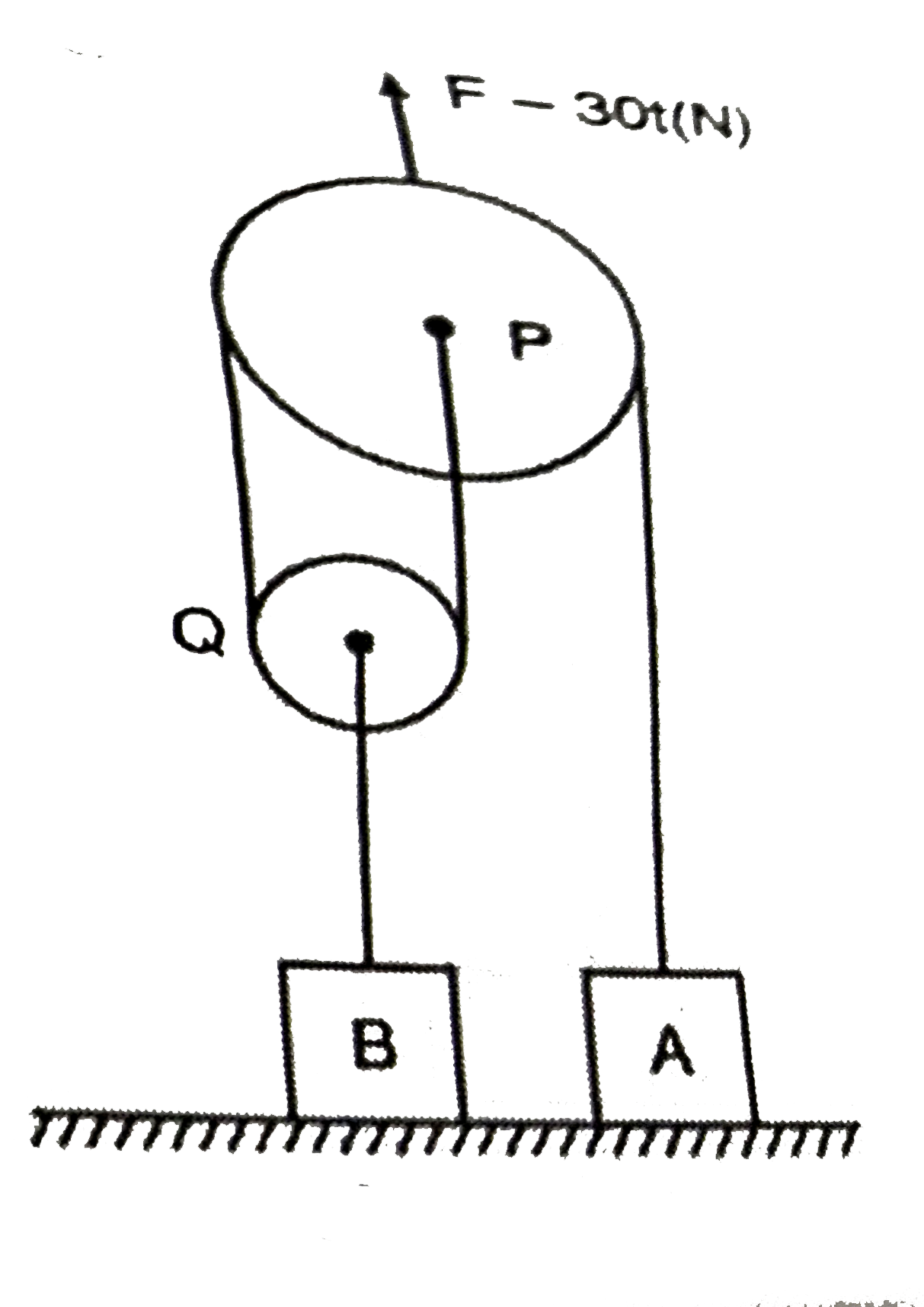
View SolutionA particle A of mass 2m is held on a smooth horizontal table and is attached to one end of an inelastic string which runs over a smooth light pulley at the edge of the table. At the other end of the string there hangs another particle B of mass m, the distance from A to the pulley is l. The particle A is then projected towards the pulley with velocity u.

(a) Find the time before the string becomes taut, and shown that after the string becomes taut, the initial velocity of A and B is 4u/3.
(b) Find the common velocity when A reaches the pulley (assume that B has not yet reached the ground).
View SolutionA light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)
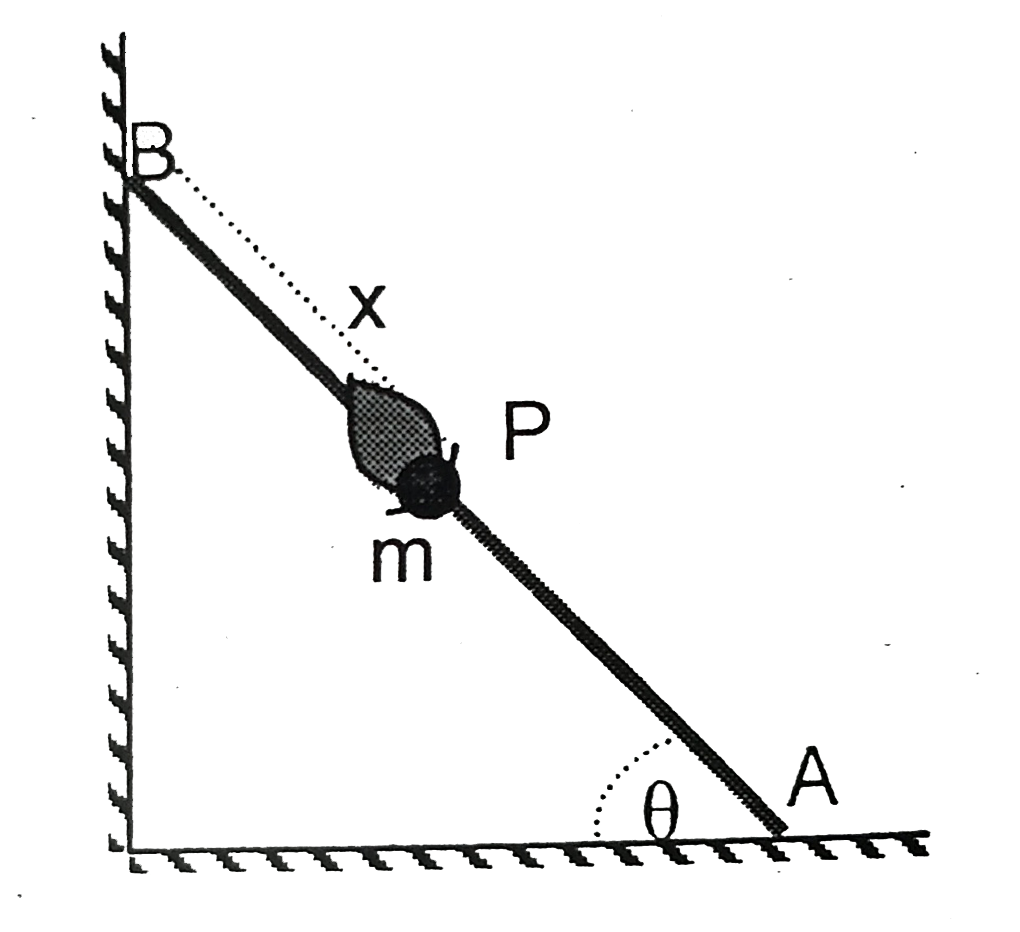
View SolutionA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
View Solution
