The equation of displacement due to a sound wave is s=s0sin^(2)((wt-kx)). if the bulk modulus of the medium is B, then the equation of pressure variation due to that sound is
Bks0sin(2ωt−2kx)
−Bks0sin(2ωt−2kx)
Bks0cos2(ωt−kx)
−Bks0cos2(ωt−kx)
The correct Answer is:A
The equation of pressure variation due to sound is
p=−Bdsdx=−Bddx[s0sin2(ωt−kx)]
=Bks0sin(2ωt−2kx)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Now answer the following :
20 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 89 illustration
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 87
6 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A sound wave is travelling in a medium.If equation of displacement wave in the medium is given by y = 2cos( 2πx −100πt + π2 ) then equation of pressure waves will be (B → Bulk modulus of medium)
(А) P= 4Bπ sin(2πx− 100πt)
(В) P= 4Bπ sin(2πx+ 100πt)
(C) P= 4Bπ cos(2πx− 100πt)
(D) P= 4Bπ cos(2πx+ 100πt)
View SolutionSpeed of sound wave in a fluid depends upon Directly on density of the medium Square of bulk modulus of the medium Inversely on the square root of density Directly on the square root of bulk modulus of the medium
View Solution
Knowledge Check
The equation of displacement due to a sound wave is s=[s0sin2(ωt−kx)]if the bulk modulus of the medium is B, then the equation of pressure variation due to that sound is
ABks0sin(2ωt−2kx)B−Bks0sin(2ωt−2kx)CBks0cos2(ωt−kx)D−Bks0cos2(ωt−kx)The equation of a sound wave is y=0.0015sin(62.4x+316t) the wavelength of this wave is
A0.2unitB0.1unitC0.3unitDcannot the calcualted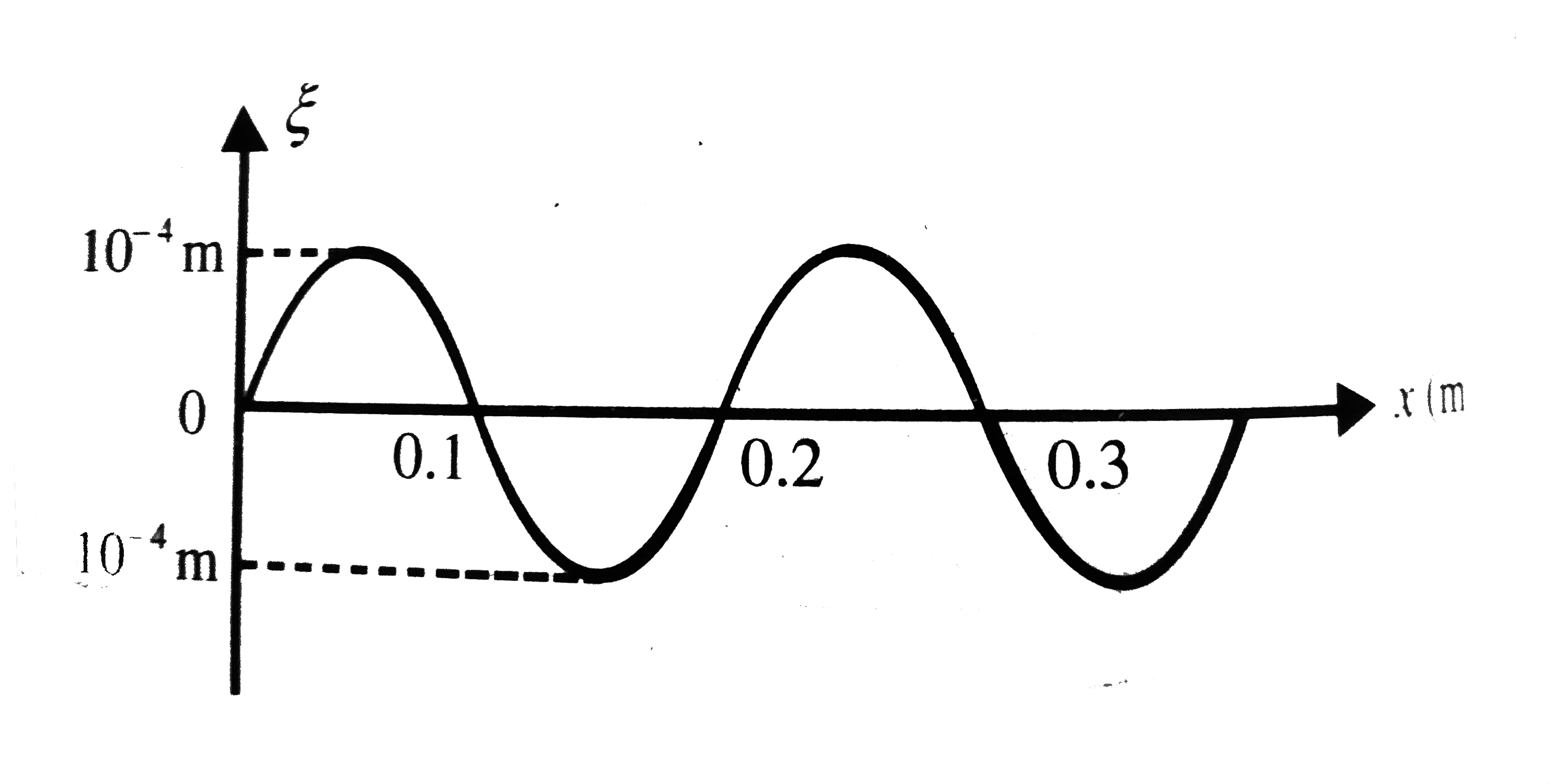
For a sound wave travelling towards +x direction, sinusoidal longitudinal displacement ε at a certain time is given as a function of x (Fig). If bulk modulus of air is B=5×105Nm2, the variation of pressure excess will beA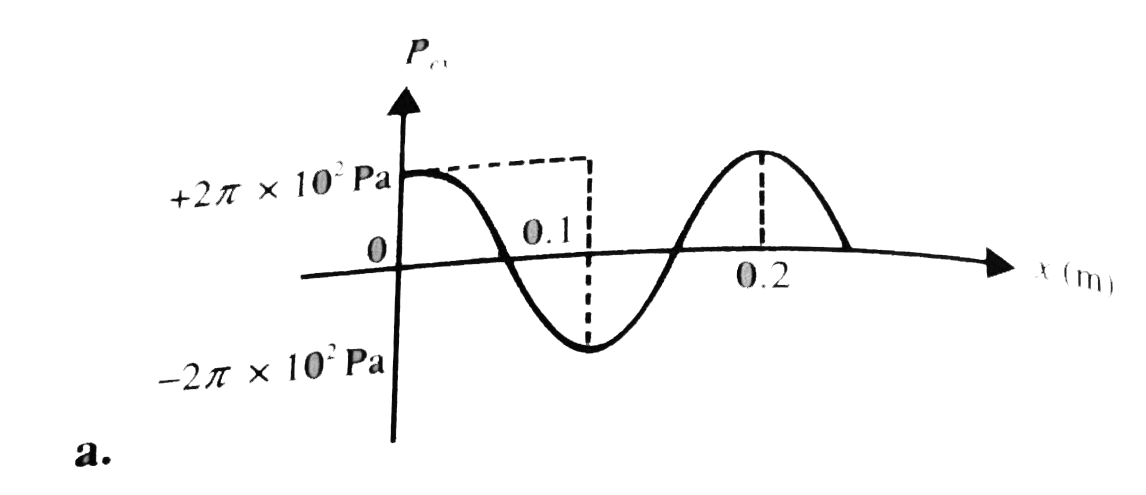 B
B C
C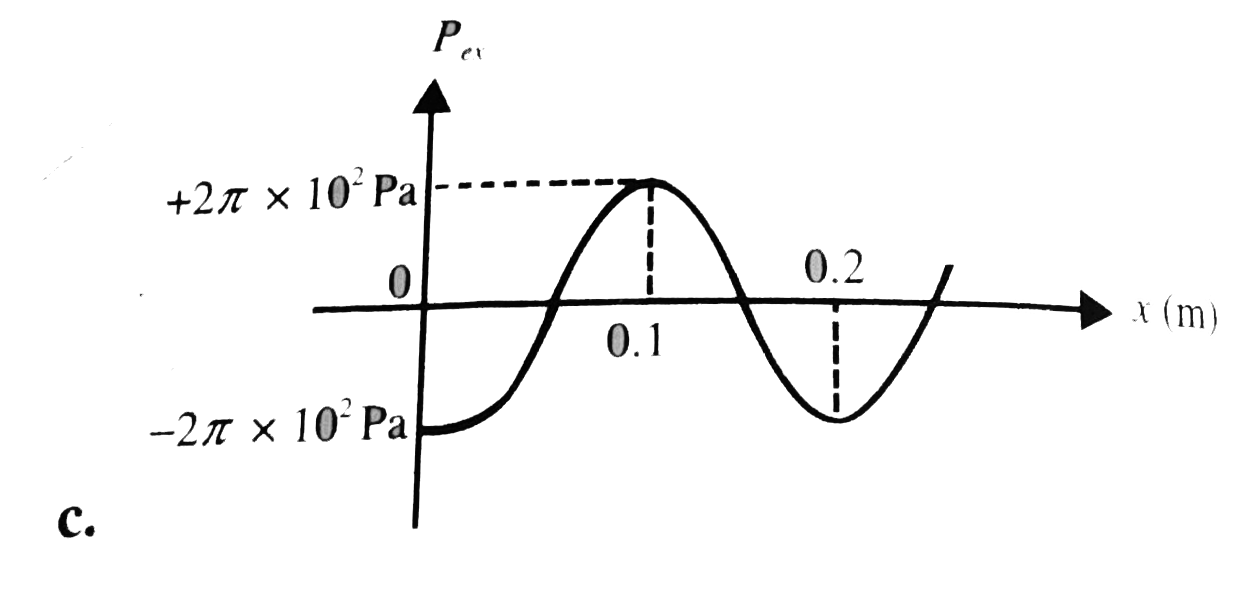 D
D
Corresponding to displacement equation,
y=Asin(kx+ωt)
of a longitudinal wave make its pressure and density wave also. Bulk modulus of the medium is B and density is p.
View SolutionSound wave pressure Equation and Displacement Equation
View SolutionThe equation of a longitudinal standing wave due to superposition of the progressive waves producted by two sources of sound is s=−20sin10πxsin100πt where s is the displacement from mean position measured in mm,x is in meters and is in seconds. The specific gravity of the medium is 10−3. Density of water =103kg/m3. Find :
(a) Wavelength, frequency and velocity of the progressive waves.
(b) Bulk modulus of the medium and the pressure amplitude.
(c) Minimum distance between pressure antinode and a displacement anotinode.
(d) Intensity at the displacement nodes.
View SolutionThe equation y=Asin2(kx−ωt) represents a wave with
View SolutionA sound wave y=Asin(ωt−kx) is propagating through a medium of density 'ρ'. Then the sound energy per unit volume is
View Solution
