A smooth rope of mas m and length L lies in a heap on a smooth horizontal floor, with one end attached to a block of mass M. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude V0 as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance x from point P as shown in figure −2(P is a point on the rope which has just started to move at the given instant ), choose correct options for next three question.

The speed of block of mass M is
mV0(M+mLx)
MV0(M+mLx)
m2V0M(M+mLx)
M2V0m(M+mLx)
The correct Answer is:B
The mass of moving material is M+mLx
From conservation of momentum MV0=(M+mLx)V
∴Velocity of moving block and moving rope is
V=MV0M+mLx
Similar Questions
If A block is dragged on a smooth horizontal plane with the help of a light rope which moves with a velocity v as given in the figure .Then find the horizontal velocity of the block .
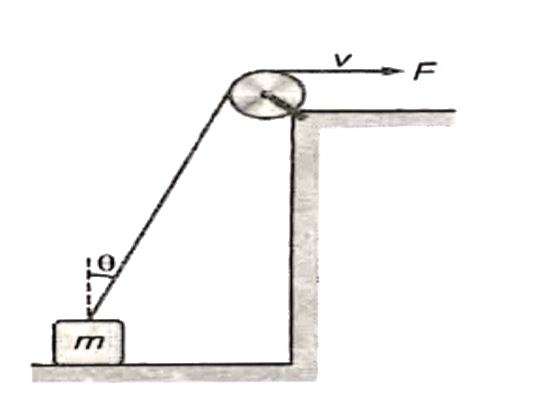
View SolutionA uniform rope of mass m and length L is attached to the ceiling of a lift. The other end of the rope is attached to a block of mass M. The lift is moving up with a constant acceleration a0. Find the tension in the rope at a distance x from the ceiling as shown in the diagram.

View Solution
Knowledge Check
A smooth rope of mas m and length L lies in a heap on a smooth horizontal floor, with one end attached to a block of mass M. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude V0 as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance x from point P as shown in figure −2(P is a point on the rope which has just started to move at the given instant ), choose correct options for next three question.

The magnitude of acceleration of block of mass M isAm3LV20(M+mLx)3BmM2LV20(M+mLx)3Cm4MLV20(M+mLx)3DM2LV20(M+mLx)3A smooth rope of mas m and length L lies in a heap on a smooth horizontal floor, with one end attached to a block of mass M. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude V0 as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance x from point P as shown in figure −2(P is a point on the rope which has just started to move at the given instant ), choose correct options for next three question.

The tension in rope at point P isAmM2LV20(M+mLx)2Bm2MLV20(M+mLx)2Cm3LV20(M+mLx)2DM3LV20(M+mLx)2A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
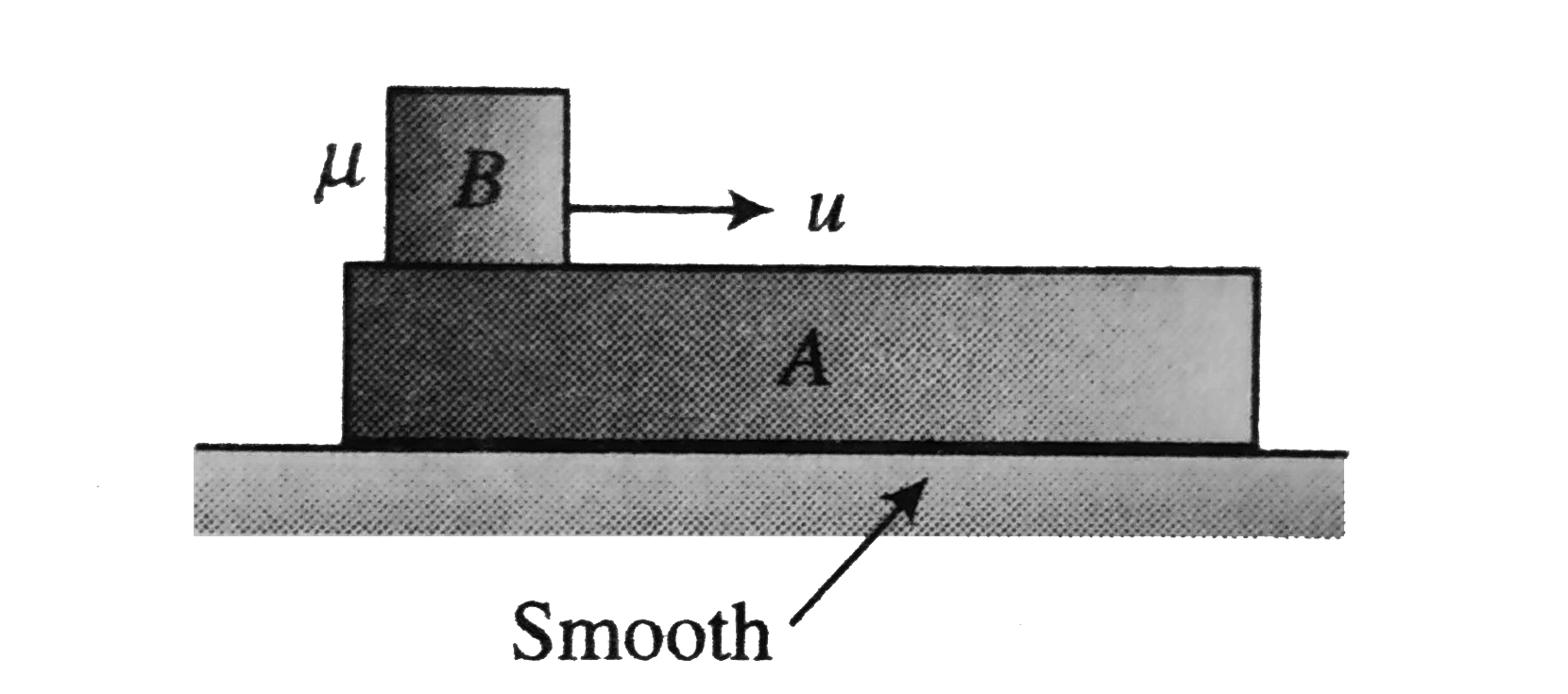 A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.
A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.
A block of mass 20 kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in the figure. Find the acceleration of the pulley
_PHY_E05_192_Q05.png)
View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :

View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA man is pulling a rope attached to a block on a smooth horizontal table. The tension in the rope will be the same at all points
View Solution
