If tan0>μ then minimum force needed to stay block at rest is

mgsinθ−μmgcosθ
mgsinθ−μmgcosθ√1+μ2
mgsinθ+μmgcosθ
Zero
The correct Answer is:B
If tanθ>μ ………….
Fcosϕ+μN=mgsinθ
N=mgcosθ+Fsinϕ
F=mgsinθ−μmgcosθμsinϕ+cosϕ
Similar Questions
A block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionA block placed on a horizotnal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started. Discuss the situation when tanθ<μ.
View Solution
Knowledge Check
A cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 . AinfinitesimalBmg/4Cmg/2Dmg(1−μ)
. AinfinitesimalBmg/4Cmg/2Dmg(1−μ)A block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 A10 NB10011NC1008ND20 N
A10 NB10011NC1008ND20 NThe minimum force required to start pushing a body up rough (frictional coefficient μ) inclined plane is F1 while the minimum force needed to prevent it from sliding down is F2. If the inclined plane makes an angle θ from the horizontal such that tan θ=2μ then the ratio F1F2 is
A4B1C2D3
A block placed on a horizotnal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started. Discuss the situation when tanθ<μ.
View SolutionFind the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View SolutionThe minimum force required to start pushing a body up a rough (frictional coefficient μ) inclined plane is F1 while the minimum force needed to prevent it from sliding down is F2. If the inclined plane makes an angle θ with the horizontal such that tanθ=2μ, then the ratio F1F2 is
View SolutionA block A of mass 100 kg rests on another block B of mass 200 kg and is tied to a wall as shown in the figure. The coefficient of friction between A and B is 0.2 and that between B and ground is 0.3. The minimum force required to move the block B is (g=10ms−2)
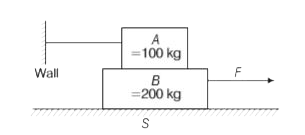
View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

View Solution
